
分析 (1)由函数f(x)的周期为3知f(5)+f(7)=f(2)+f(1)=4+4+1+4=13;
(2)x∈[4,6]时,f(x)=f(x-3)=(x-3)2+4;从而化简方程f(x)=mx2为(x-3)2+4=mx2,从而得到m=$\frac{{x}^{2}-6x+13}{{x}^{2}}$=13($\frac{1}{x}$-$\frac{3}{13}$)2+$\frac{4}{13}$,从而解得.
解答 解:(1)∵函数f(x)的周期为3,
∴f(5)+f(7)=f(2)+f(1)=4+4+1+4=13;
(2)x∈[4,6]时,f(x)=f(x-3)=(x-3)2+4;
故方程f(x)=mx2可化为(x-3)2+4=mx2,
故m=$\frac{{x}^{2}-6x+13}{{x}^{2}}$
=13($\frac{1}{x}$-$\frac{3}{13}$)2+$\frac{4}{13}$,
∵4≤x≤6,
∴$\frac{4}{13}$≤13($\frac{1}{x}$-$\frac{3}{13}$)2+$\frac{4}{13}$≤$\frac{13}{36}$,
即$\frac{4}{13}$≤m≤$\frac{13}{36}$.
点评 本题考查了函数的性质的应用及独立系数法求取值范围,属于基础题.


科目:高中数学 来源: 题型:解答题
 某企业员工共500人参加“学雷锋”志愿活动,按年龄分组:第一组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.
某企业员工共500人参加“学雷锋”志愿活动,按年龄分组:第一组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 计划购物情况 | 没有计划购物 | 计划购物1000元以内(不含1000元) | 计划购物1000元以上(含1000元) |
| 所占比例 | $\frac{1}{5}$ | $\frac{2}{3}$ | x |
| A. | 100 | B. | 200 | C. | 300 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
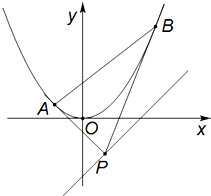 已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,
已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32π | B. | 16π | C. | 12π | D. | $\frac{32}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com