
 如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )
如图,正方体ABCD-A1B1C1D1的棱长为2$\sqrt{3}$,以顶点A为球心,4为半径作一个球,则图中球面与正方体的表面相交所得的两段弧长之和等于( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{7π}{6}$ |
分析 球面与正方体的六个面都相交,所得的交线分为两类:一类在顶点A所在的三个面上,即面AA1B1B、面ABCD和面AA1D1D上;另一类在不过顶点A的三个面上,即面BB1C1C、面CC1D1D和面A1B1C1D1上.由空间几何知识能求出这两段弧的长度之和.
解答  解:如图,球面与正方体的六个面都相交,
解:如图,球面与正方体的六个面都相交,
所得的交线分为两类:一类在顶点A所在的三个面上,即面AA1B1B、面ABCD和面AA1D1D上;
另一类在不过顶点A的三个面上,即面BB1C1C、面CC1D1D和面A1B1C1D1上.
在面AA1B1B上,交线为弧EF且在过球心A的大圆上,因为AE=4,AA1=2$\sqrt{3}$,
则∠A1AE=$\frac{π}{6}$.同理∠BAF=$\frac{π}{6}$,所以∠EAF=$\frac{π}{6}$,
故弧EF的长为:4×$\frac{π}{6}$=$\frac{2π}{3}$,
而这样的弧共有三条.
在面BB1C1C上,交线为弧FG且在距球心为1的平面与球面相交所得的小圆上,
此时,小圆的圆心为B,半径为2,∠FBG=$\frac{π}{2}$,
所以弧FG的长为:1×$\frac{π}{2}$=$\frac{π}{2}$.
于是,所得的曲线长为:$\frac{2π}{3}$+$\frac{π}{2}$=$\frac{7π}{6}$.
故选:D.
点评 本题考查空间几何的性质和综合应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业员工共500人参加“学雷锋”志愿活动,按年龄分组:第一组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.
某企业员工共500人参加“学雷锋”志愿活动,按年龄分组:第一组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
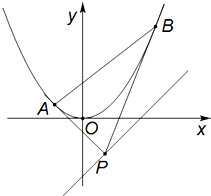 已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,
已知直线l的方程是y=x-1和抛物线C:x2=y,自l上任意一点P作抛物线的两条切线,设切点分别为A,B,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{127}{64}$ | C. | $\frac{9}{4}$ | D. | $\frac{129}{64}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com