
分析 (1)直接利用复数的代数形式的混合运算化简求解即可求.
(2)化简z2+az+b=1-i,然后利用复数相等列出方程组,即可求实数a,b的值
解答 解:(1)(2-i)(-1+5i)(3+4i)+2i=(3+11i)(3+4i)+2i=-35+45i+2i=-35+47i,
(2)z=(1-i)2+1+3i=-2i+1+3i=1+i,
由z2+az+b=1-i,得(a+b)+(2+a)i=1-i,
∴$\left\{\begin{array}{l}{a+b=1}\\{2+a=-1}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-3}\\{b=4}\end{array}\right.$,
∴实数对(a,b)的值为(-3,4).
点评 本题考查复数的代数形式的混合运算,复数相等的条件的应用,考查计算能力.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.
如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
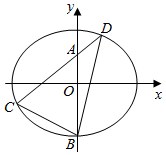 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45°,点E,F分别是AC,AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45°,点E,F分别是AC,AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com