
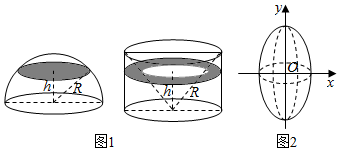
���� ����һ������뾶Ϊ2����Ϊ5��Բ����������ȥһ��Բ�������敜ԭ���ɵã���������Ϊ�����������2����
��� �⣺��Բ�ij�����Ϊ5���̰���Ϊ2��
�ֹ���һ������뾶Ϊ2����Ϊ5��Բ����Ȼ����Բ������ȥһ����Բ���µ���Բ��Ϊ���㣬Բ���ϵ���Ϊ�����Բ��
�����敜ԭ���ó���������V=2��VԲ��-VԲ��=2���С�22��5-$\frac{1}{3}�С�{2}^{2}��5$��=$\frac{80��}{3}$��
�ʴ�Ϊ��$\frac{80��}{3}$��
���� ���⿼���˶��敜ԭ�������⣬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��3�� | B�� | ��-1��3�� | C�� | {2} | D�� | {-1��2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2-3i | B�� | -2+3i | C�� | 2-3i | D�� | 2+3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 6 | C�� | -3 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${x^2}+\frac{1}{x^2}��x+\frac{1}{x}$ | B�� | $\sqrt{x+3}-\sqrt{x+1}��\sqrt{x+2}-\sqrt{x}$ | C�� | $|x-y|+\frac{1}{x-y}��2$ | D�� | |x-y|��|x-z|+|y-z| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com