
分析 (1)求出函数的导数,代入f′(2)=0,求出m的值,从而求出切线方程即可;
(2)问题转化为y=ex和y=mx在(0,+∞)有交点,通过讨论m的范围,结合曲线的切线方程求出m的具体范围即可.
解答 解:(1)f(x)=$\frac{{e}^{x}}{{x}^{2}}$-$\frac{m}{x}$,f′(x)=$\frac{{e}^{x}(x-2)}{{x}^{3}}$+$\frac{m}{{x}^{2}}$,
若f(x)在x=2处取得极值,则f′(2)=$\frac{m}{4}$=0,
解得:m=0,
∴f(x)=$\frac{{e}^{x}}{{x}^{2}}$,f′(x)=$\frac{{e}^{x}(x-2)}{{x}^{3}}$,
f(1)=e,f′(1)=-e,
故切线方程是:y-e=-e(x-1),即:ex+y-2e=0;
(2)若x∈(0,+∞)时方程f(x)=0有实数根,
即方程ex=mx在(0,+∞)有实数根,
即y=ex和y=mx在(0,+∞)有交点,
显然m≤0时,无交点,
m>0时,若y=ex和y=mx相切,设切点是(x0,${e}^{{x}_{0}}$),
故切线的斜率m=k=${e}^{{x}_{0}}$,
则得到${e}^{{x}_{0}}$=${e}^{{x}_{0}}$x0,解得:x0=1,
∴m=k=${e}^{{x}_{0}}$=e,
故m≥e.
点评 本题考查了切线方程问题,考查函数的极值以及函数交点问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(-π)>f(log2$\frac{1}{4}$)>f($-\frac{π}{2}$) | B. | f(log2$\frac{1}{4}$)>f(-$\frac{π}{2}$)>f(-π) | ||
| C. | f(-π)>f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$) | D. | f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$)>f(-π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
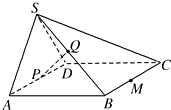 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE是等边三角形,AE⊥BE,M为CE上一点,且BM⊥平面ACE.
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE是等边三角形,AE⊥BE,M为CE上一点,且BM⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
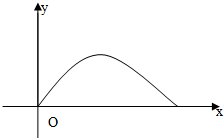 如图,在平面直角坐标系xOy中,x轴在地平面上,y轴垂直于地面,x轴、y轴上的单位长度都为1km,某炮位于坐标原点处,炮弹发射后,其路径为抛物线y=kx-$\frac{1}{20}(1+{k^2}){x^2}$的一部分,其中k与炮弹的发射角有关且k>0.
如图,在平面直角坐标系xOy中,x轴在地平面上,y轴垂直于地面,x轴、y轴上的单位长度都为1km,某炮位于坐标原点处,炮弹发射后,其路径为抛物线y=kx-$\frac{1}{20}(1+{k^2}){x^2}$的一部分,其中k与炮弹的发射角有关且k>0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9万元 | B. | 8万元 | C. | 7万元 | D. | 6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{10}^{3}$种 | B. | C${\;}_{10}^{3}$ 种 | ||
| C. | C${\;}_{10}^{3}$A${\;}_{10}^{3}$种 | D. | 30 种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com