
分析 (Ⅰ)利用独立重复试验的概率公式,求考生甲至少正确完成2道题的概率;
(Ⅱ)确定基本事件数,即可求出考生乙能通过笔试进入面试的概率;
(Ⅲ)确定ξ的可能取值,求出相应的概率,即可求ξ的分布列和数学期望.
解答 解:(Ⅰ)设考生甲至少正确完成2道题的概率为P,则P=${C}_{3}^{2}(\frac{2}{3})^{2}•\frac{1}{3}+{C}_{3}^{3}(\frac{2}{3})^{3}$=$\frac{20}{27}$;
(Ⅱ)基本事件总数为${C}_{6}^{3}$=20,考生乙能通过笔试进入面试的基本事件数为${C}_{4}^{3}+{C}_{4}^{2}{C}_{2}^{1}$=16,
所以考生甲至少正确完成2道题的概率为$\frac{16}{20}$=$\frac{4}{5}$;
(Ⅲ)ξ的所有可能取值为1,2,3,则
P(ξ=1)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,P(ξ=2)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,P(ξ=3)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,是历年高考的必考题型.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.
设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$
将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
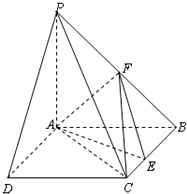 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 甲电池待机时间(h) | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
| 乙电池待机时间(h) | 118 | 123 | 127 | 120 | 124 | 120 | 122 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.
如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com