
| A. | $({0,\;\frac{1}{2}}]$ | B. | $({0,\;\frac{1}{3}}]$ | C. | $({0,\;\frac{1}{4}}]$ | D. | $[{\frac{1}{4},\;\;\frac{1}{3}}]$ |
分析 在同一平面直角坐标系中画出函数y=f(x)和函数y=k(x+1)的图象,数形结合可得答案.
解答 解:由f(-x)=f(x),知函数f(x)为偶函数;
由$f({x+1})=-\frac{1}{f(x)}$,得函数f(x)的周期为2.
又∵$f({-x+1})=-\frac{1}{{f({-x})}}=-\frac{1}{f(x)}$,∴f(-x+1)=f(x+1),∴函数f(x)的图象关于x=1对称.
令g(x)=f(x)-k(x+1)=0,得f(x)=k(x+1).
在同一平面直角坐标系中画出函数y=f(x)和函数y=k(x+1)的图象,如图,
由图可知,当直线y=k(x+1)过点C(3,1)时有4个交点,
此时直线y=k(x+1)的斜率为$k=\frac{1-0}{{3-({-1})}}=\frac{1}{4}$,
要使函数g(x)=f(x)-k(x+1)有4个零点,
则直线的斜率满足$0<k≤\frac{1}{4}$..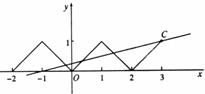
故选:C
点评 本题考查的知识点是数形结合思想,转化思想,函数的零点,函数的图象,难度中档.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 归纳推理,类比推理 | B. | 演绎推理,类比推理 | ||
| C. | 类比推理,演绎推理 | D. | 归纳推理,演绎推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-∞,0)∪(3,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,4) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{26}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
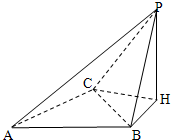 如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
如图,在四面体P-ABC,底面ABC是边长为1的正三角形,AB⊥BP,点P在底面ABC上的射影为H,BH=$\frac{\sqrt{3}}{3}$,平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com