练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等差数列{an}中，a9=
    1
    2
    a12+6    ，则数列{an}的前11项和S11等于
     
    ．
    考点：等差数列的前n项和
    专题：等差数列与等比数列
    分析：由已知条件，利用等差数列的通项公式推导出a1+5d=12，由此利用等差数列的前n项和公式能求出S11．
    解答： 解：∵等差数列{an}中，a9=
    1
    2
    a12+6    ，即2a9=a12+12，
    ∴2（a1+8d）=a1+11d+12，
    ∴a1+5d=12，
    ∴S11=
    11
    2
    （a1+a11）
    =
    11
    2
    （2a1+10d）
    =11（a1+5d）
    =11×12
    =132．
    故答案为：132．
    点评：本题考查数列的前11项和的求法，是基础题，解题时要熟练掌握等差数列的通项公式和前n项和公式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知|
    a
    |=4，
    e
    为单位向量，当
    a
    ，
    e
    的夹角为
    2π
    3
    时，
    a
    +
    e
    在
    a
    -
    e
    上的投影为（　　）
    A、5
    B、
    15
    4
    C、
    15
    		13
    13
    D、
    5
    		21
    7

    查看答案和解析>>

    科目：高中数学 来源： 题型：

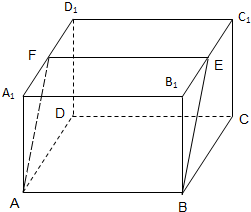    如图，直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形，∠BAD=60°，高为1，过底边AB作一截面ABEF，若BE=2
    （1）求二面角E-AB-C的大小；
    （2）求截面ABEF的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=f（x）的图象在点P（3，f（3））处的切线方程为y=x+2，f′（x）为f（x）的导函数，则f（3）+f′（3）
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，矩形ABEF和正方形ABCD有公共边AB，它们所在平面成60°的二面角，AB=CB=2a，BE=a，则DE=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设m，n为不重合的两条直线，α，β为不重合的两个平面，给出下列命题：
    ①若m∥α，m∥β，则α∥β；    
    ②若l∥α，m∥β，α∥β，则l∥m；
    ③若m⊥α，n⊥α，则m∥n；      
    ④若m⊥n，m⊥α，则n⊥α．
    则其中所有真命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法不正确的是（　　）
    A、所有的对立事件都是互斥事件
    B、先后抛掷两枚大小一样的硬币，两枚都出现反面的概率是
    1
    3
    C、事件“直线y=k（x+1）过点（-1，0）”是必然事件
    D、某红绿灯路口，红灯时间为30秒，黄灯时间为5秒，绿灯时间为45秒，当你到这个路口时，看到黄灯的概率是
    1
    16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中的假命题是（　　）
    A、?x∈R，2x-1＞0
    B、?x∈R，lgx＜1
    C、?x∈N+，（x-1）2＞0
    D、?x∈R，tanx=2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

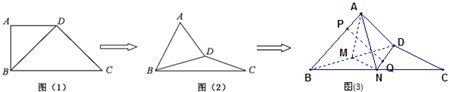    在直角梯形ABCD中，AD∥BC，BC=2AD=2AB=2
    		2
    ，∠ABC=90°（如图1）．把△ABD沿BD翻折，使得二面角A-BD-C的平面角为θ（如图2）
    （1）若θ=
    π
    2
    ，求证：CD⊥AB；
    （2）是否存在适当θ的值，使得AC⊥BD，若存在，求出θ的值，若不存在说明理由；
    （3）若θ=
    π
    2
    ，取BD中点M，BC中点N，P、Q分别为线段AB与DN上一点，使得
    AP
    PB
    =
    NQ
    QD
    =λ(λ∈R)    ．令PQ与BD和AN所成的角分别为θ1和θ2．求sinθ1+sinθ2的最大值．

    查看答案和解析>>

    同步练习册答案