
| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{8}{5}$ |
分析 确定AB的方程,求出S△ADN、SACME.利用P(x,y)在椭圆上可知S1=S2,从而可得结论.
解答 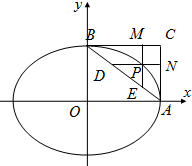 解:设P(x,y)在第一象限,则AB的方程为$\frac{x}{5}$+$\frac{y}{3}$=1,
解:设P(x,y)在第一象限,则AB的方程为$\frac{x}{5}$+$\frac{y}{3}$=1,
∴D(5-$\frac{5y}{3}$,y),E(x,3-$\frac{3x}{5}$),
∴S△ADN=$\frac{1}{2}$×$y×\frac{5y}{3}$=$\frac{5{y}^{2}}{6}$,
∴SACME=$\frac{1}{2}×$($\frac{3x}{5}+3$)×(5-x)=$\frac{3}{10}$(25-x2),
∵P(x,y)在椭圆上,∴$\frac{x^2}{25}+\frac{y^2}{9}=1$,
∴y2=9-$\frac{9{x}^{2}}{25}$,
∴$\frac{5{y}^{2}}{6}$=$\frac{3}{10}$(25-x2),
∴S△ADN=SACME,
∴S1=S2,
∴$\frac{{2{S_1}}}{S_2}$=2.
故选A.
点评 本题考查椭圆的标准方程,考查面积的计算,考查学生的计算能力,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{5\sqrt{3}π}}{6}+6$ | B. | $\sqrt{3}π+7$ | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com