考点:棱柱、棱锥、棱台的侧面积和表面积,异面直线及其所成的角
专题:空间位置关系与距离
分析:(Ⅰ)过A1作A1H⊥平面ABC,垂足为H.过H作HD⊥AB,连A1D,通过三角形全等,说明H在∠CAB平分线AE上,然后推出异面直线AA1与BC所成的角;
(Ⅱ)利用第一问的结果,直接求解此棱柱的表面积和体积.
解答:
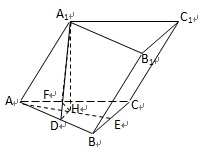
解:(Ⅰ)过A
1作A
1H⊥平面ABC,垂足为H.
过H作HD⊥AB,连A
1D则A
1D⊥AB
作HF⊥AC,连结A
1F则A
1F⊥AC,又∠A
1AB=∠A
1AC=45°
∴Rt△DAA
1≌Rt△FAA
1,∴AD=AF∴Rt△ADH≌Rt△FAH
所以H在∠CAB平分线AE上,由△ABC为正三角形,
∴BC⊥AE⇒BC⊥AA
1异面直线AA
1与BC所成角为90°;-------------(7分)
(未证明H在∠CAB平分线AE上,扣3分)
(Ⅱ)由(Ⅰ)知在直角三角形A
1AD中,计算得A
1D=AD=1,
在Rt△ADH中,计算得DH=
在Rt△A
1DH中,计算得
A1H=,
∴
S=2S△ABC+SBCC1B1=
+2+.
V=S
△ABC•A
1H=
×=---------------------(14分)
点评:本题考查异面直线所成角的求法,几何体的体积与部门决定求法,考查空间想象能力以及计算能力.

 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为 解:(Ⅰ)过A1作A1H⊥平面ABC,垂足为H.
解:(Ⅰ)过A1作A1H⊥平面ABC,垂足为H.

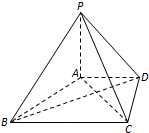 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=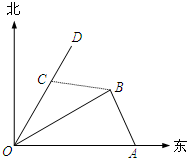 如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.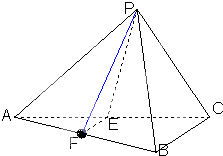 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.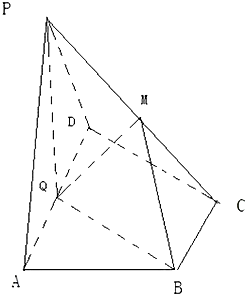 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=