
分析 (I)由an+1=2an+1,变形为:an+1+1=2(an+1),且a1+1=6≠0,利用等比数列的通项公式及其定义即可得出;
(II)由nan=n(3•2n-1),数列{nan}的前n项和Sn=3(2+2×22+3×23+…+n×2n)-(1+2+3+…+n),利用“错位相减法”、等比数列与等差数列的前n项和公式即可得出.
解答 (I)证明:∵an+1=2an+1,
∴an+1+1=2(an+1),且a1+1=6≠0,∴$\frac{{{a_{n+1}}+1}}{{{a_n}+1}}$=2,﹍﹍﹍﹍﹍﹍﹍﹍﹍(3分)
∴数列{an+1}是以6为首项,2为公比的等比数列,﹍﹍﹍﹍﹍﹍﹍﹍﹍(4分)
∴an+1=(a1+1)•2n-1=6•2n-1=3•2n,
∴an=3•2n-1.﹍﹍﹍﹍﹍﹍﹍﹍﹍(6分)
(II)∵nan=n(3•2n-1),
数列{nan}的前n项和Sn=3(2+2×22+3×23+…+n×2n)-(1+2+3+…+n),
令Tn=2+2×22+3×23+…+n×2n,
∴2Tn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1,
∴-Tn=2+22+23+…+2n-n•2n+1
=$\frac{{2(1-{2^n})}}{1-2}$-n•2n+1=-(n-1)•2n+1-2,
∴Tn=(n-1)•2n+1+2,﹍﹍﹍﹍﹍﹍﹍﹍﹍(10分)
∴Sn=3(n-1)•2n+1-$\frac{n(n+1)}{2}$+6.﹍﹍﹍﹍﹍﹍﹍﹍﹍(12分)
点评 本题考查了数列的递推关系、“错位相减法”、等比数列与等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )| A. | 向左平移$\frac{π}{8}$个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 向右平移$\frac{π}{8}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变 | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变 | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
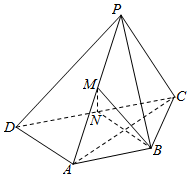 如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.
如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com