
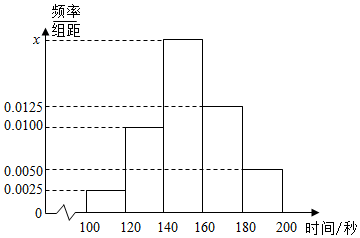
���� ��1����Ƶ�ʷֲ�ֱ��ͼ�������x���ɴ������������������б���˺ϸ��Ա��������
��2������֪����2���е㳮��ʱ����120�������X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ���ã�
��0.0025+0.0100+x+0.0125+0.0050����20=1��
���x=0.02��
������������б���˺ϸ��Ա������Ϊ��
��0.0025+0.0100+0.0200����20��200=130���ˣ���
��2�����˺ϸ��130���У��㳮��ʱ����120�������Ϊ0.0025��20��200=10��
�Ӹ����б���˺ϸ��ȫ��Ա������ѡ2�ˣ���2���е㳮��ʱ����120�������X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=$\frac{{C}_{120}^{2}}{{C}_{130}^{2}}$=$\frac{476}{559}$��
P��X=1��=$\frac{{C}_{120}^{1}{C}_{10}^{1}}{{C}_{130}^{2}}$=$\frac{80}{559}$��
P��X=2��=$\frac{{C}_{10}^{2}}{{C}_{130}^{2}}$=$\frac{3}{559}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{476}{559}$ | $\frac{80}{559}$ | $\frac{3}{559}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | 6 | C�� | -$\frac{1}{6}$ | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ab-3a-b=0 | B�� | ab-a-3b=0 | C�� | ab-a-b=0 | D�� | ab+a-b=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+1 | B�� | 2 | C�� | 2$\sqrt{2}$+2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -$\frac{1}{2}$ | C�� | $\frac{1}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
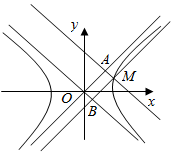 ��ͼ����MΪ˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������һ�㣬OΪԭ�㣬����M��˫�����������ߵ�ƽ���ߣ��ֱ����������߽���A��B���㣬̽��ƽ���ı���MAOB��������ɴ˿��Է���ʲô���ۣ�
��ͼ����MΪ˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������һ�㣬OΪԭ�㣬����M��˫�����������ߵ�ƽ���ߣ��ֱ����������߽���A��B���㣬̽��ƽ���ı���MAOB��������ɴ˿��Է���ʲô���ۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com