
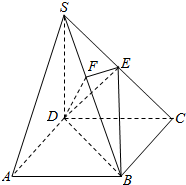
 如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.分析 (1)连接AC交BD于点O,连接OE.然后利用三角形中位线的性质可得OE∥SA,再由线面平行的判定定理证得SA∥平面BDE;
(2)由SD=DC,E是SC的中点可得DE⊥SC,再由面面垂直的判定和性质得到BC⊥平面SDC,从而得到BC⊥DE,进一步得到SB⊥DE,结合已知EF⊥SB,由线面垂直的判定得结论;
(3)根据二面角的定义得到∠EFD是二面角C-SB-D的平面角,根据三角形的边角关系进行求解即可.
解答 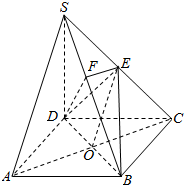 (1)证明:如图,
(1)证明:如图,
连接AC交BD于点O,连接OE.
∵点O、E分别为AC、SC的中点,
∴OE∥SA,又OE?平面BDE,SA?平面BDE,
∴SA∥平面BDE;
(2)证明:∵SD=DC,E是SC的中点,∴DE⊥SC,
又SD⊥底面ABCD,∴平面SDC⊥平面ABCD,
∵底面ABCD是矩形,∴BC⊥平面SDC,
∴BC⊥DE,
又SC∩BC=C,∴DE⊥平面SBC,
又SB?平面SBC,∴SB⊥DE,
又EF⊥SB,
EF∩ED=E,
∴SB⊥平面EFD;
(3)∵EF⊥SB,SB⊥平面EFD,
∴∠EFD是二面角C-SB-D的平面角,
设AD=1,则SD=CD=2,
则SC=2$\sqrt{2}$,SB=$\sqrt{B{C}^{2}+S{C}^{2}}$=3,BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{1+4}$=$\sqrt{5}$,DE=$\sqrt{2}$,
在三角形SDB中,SB•DF=SD•BD,即DF=$\frac{SD•BD}{SB}$=$\frac{2×\sqrt{5}}{3}$=$\frac{2\sqrt{5}}{3}$,
在三角形SBC中,sinCSB=$\frac{BC}{SB}=\frac{EF}{SE}=\frac{1}{3}$,即EF=$\frac{1}{3}$SE=$\frac{\sqrt{2}}{3}$,
在三角形DEF中,cosEFD=$\frac{E{F}^{2}+D{F}^{2}-D{E}^{2}}{2EF•DF}$=$\frac{(\frac{\sqrt{2}}{3})^{2}+(\frac{2\sqrt{5}}{3})^{2}-(\sqrt{2})^{2}}{2×\frac{\sqrt{2}}{3}×\frac{2\sqrt{5}}{3}}$=$\frac{\frac{2}{9}+\frac{20}{9}-2}{\frac{4\sqrt{10}}{9}}$=$\frac{22-18}{4\sqrt{10}}=\frac{4}{4\sqrt{10}}=\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$,
即二面角C-SB-D的余弦值是$\frac{\sqrt{10}}{10}$.
点评 本题综合考查空间中线线、线面的位置关系和空间中角的计算,涉及二面角的平面角,传统方法和坐标向量法均可,考查的知识面较广,综合性较强,运算量较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
已知函数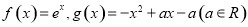 ,点
,点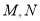 分别在
分别在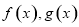 的图象上.
的图象上.
(1)若函数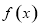 在
在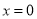 处的切线恰好与
处的切线恰好与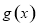 相切,求
相切,求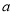 的值;
的值;
(2)若点 的横坐标均为
的横坐标均为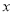 ,记
,记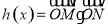 ,当
,当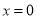 时,函数
时,函数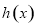 取得极大值,求
取得极大值,求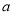 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
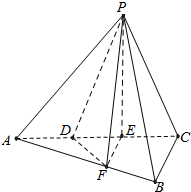 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+$\sqrt{17}$ | B. | 3+$2\sqrt{5}$ | C. | $\frac{19}{2}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
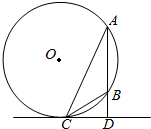 如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
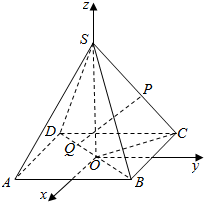 在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.
在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com