
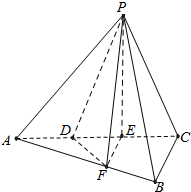
 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.分析 (1)由EF∥面PBC可得出EF∥BC;
(2)由PC=PD=CD=4可知△PDC是等边三角形,故PE⊥AC,由平面PAC⊥平面ABC可得PE⊥平面ABC,故PE⊥AB,由EF∥BC,BC⊥AB可得AB⊥EF,从而AB⊥平面PEF;
(3)设BC=x,用x表示出四边形DFBC的面积,根据体积列出方程解出x.
解答 解:(1)证明:∵EF∥面PBC.EF?面ABC,面PBC∩面ABC=BC,
∴EF∥BC.
(2)∵由CD=DE+EC=4,PD=PC=4,∴△PDC是等边三角形,
∴PE⊥AC,又∵平面PAC⊥平面ABC,平面PAC∩面ABC=AC,PE?平面PAC,
∴PE⊥平面ABC,∵AB?平面ABC,
∴PE⊥AB,
∵∠ABC=$\frac{π}{2}$,EF∥BC.∴AB⊥EF,
又∵PE?平面PEF,EF?平面PEF,PE∩EF=E,
∴AB⊥平面PEF.
(3)设BC=x,则AB=$\sqrt{36-{x^2}}$,∴${S_{△ABC}}=\frac{1}{2}AB•BC$=$\frac{x}{2}$$\sqrt{36-{x}^{2}}$,
∵EF∥BC,∴△AFE∽△ABC,∴${S_{△AEF}}:{S_{△ABC}}=\frac{4}{9}$.
∵AD=$\frac{1}{2}$AE,${S_{△AFD}}=\frac{1}{9}x\sqrt{36-{x^2}}$,∴S四边形DFBC=$\frac{7}{18}x\sqrt{36-{x^2}}$,
由(2)可知PE⊥平面ABC,且PE=$2\sqrt{3}$,
∴V=$\frac{1}{3}×\frac{7}{18}x\sqrt{36-{x^2}}×2\sqrt{3}=7$,解得x=3或者$x=3\sqrt{3}$,
∴BC=3或BC=$3\sqrt{3}$.
点评 本题考查了线面平行的性质,线面垂直的判定,棱锥的体积计算,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
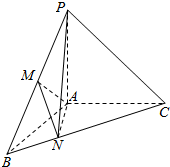 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
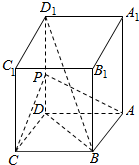 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
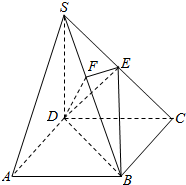 如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
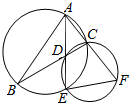 如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.
如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
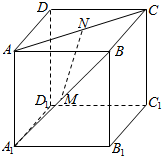 如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
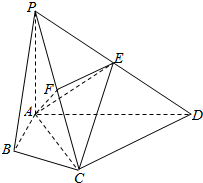 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com