
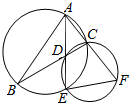
 如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.
如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.分析 (1)证明∠ECF=∠EFC,即可证明EC=EF;
(2)证明△CEA∽△DEC,求出EA,利用割线定理,即可求AC•AF的值.
解答 (1)证明:因为∠ECF=∠CAE+∠CEA=∠CAE+∠CBA,∠EFC=∠CDA=∠BAE+∠CBA,AE平分∠BAC,
所以∠ECF=∠EFC,所以EC=EF.---(4分)
(2)解:因为∠ECD=∠BAE=∠EAC,∠CEA=∠DEC,
所以△CEA∽△DEC,即$\frac{CE}{EA}=\frac{DE}{CE},EA=\frac{{E{C^2}}}{DE}$,---(6分)
由(1)知,EC=EF=3,所以$EA=\frac{9}{2}$,---(8分)
所以$AC•AF=AD•AE=(AE-DE)•AE=\frac{45}{4}$.---(10分)
点评 本题考查三角形相似的判定与性质,考查割线定理,考查学生的计算能力,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
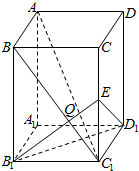 如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.
如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
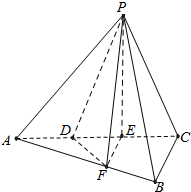 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 150° | C. | 30°或150° | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+$\sqrt{17}$ | B. | 3+$2\sqrt{5}$ | C. | $\frac{19}{2}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
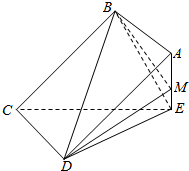 如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD
如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com