
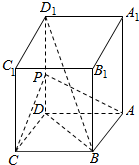
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.分析 (1)由知得PD⊥平面ACD,PD=1,由此能求出三棱锥P-ACD的体积.
(2)设点D到平面PAC的距离为h,由VD-PAC=VP-ACD,能求出点D到平面PAC的距离.
解答 解:(1)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,
∴PD⊥平面ACD,PD=1,${S}_{△ACD}=\frac{1}{2}×1×1$=$\frac{1}{2}$,
∴三棱锥P-ACD的体积V=$\frac{1}{3}×{S}_{△ACD}×PD$=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
(2)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,
∴PC=PA=$\sqrt{1+1}$=$\sqrt{2}$,AC=$\sqrt{1+1}$=$\sqrt{2}$,
∴${S}_{△PAC}=\frac{1}{2}×\sqrt{2}×\sqrt{2}×sin60°$=$\frac{\sqrt{3}}{2}$,
设点D到平面PAC的距离为h,
∵VD-PAC=VP-ACD,
∵三棱锥P-ACD的体积V=$\frac{1}{6}$.
∴$\frac{1}{3}×{S}_{△PAC}×h=\frac{1}{6}$,
∴h=$\frac{\frac{1}{6}}{\frac{1}{3}×\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$.
∴点D到平面PAC的距离为$\frac{\sqrt{3}}{3}$.
点评 本题考查三棱锥的体积的求法,考查点到平面的距离的求法,是基础题,解题时要认真审题,注意等体积法的合理运用.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:选择题
若关于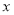 的方程
的方程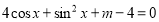 恒有实数解,则实数
恒有实数解,则实数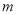 的取值范围是( )
的取值范围是( )
A. 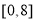 B.
B. 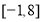 C.
C.  D.
D. 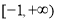
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
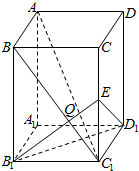 如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.
如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
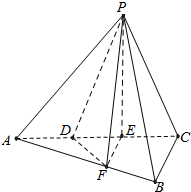 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 150° | C. | 30°或150° | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
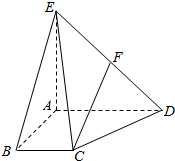 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com