
分析 (1)分别根据导数和平均速度和瞬时速速的关系即可求出;
(1)先求导,再代值即可.
解答 解:(1)①△s=s(2)-s(1)=-4+20+1-10=17,△t=2-1=1
∴$\frac{△s}{△t}$=17,
∴物体在1到2秒间的平均速度为17,
②△s=s(1+△t)-s(1)=-(1+△t)2+10(1+△t)+1-10=8△t-△t2,
∴$\frac{△s}{△t}$=8-△t,
∴物体在1到1+△t秒间的平均速度为8-△t,
③S′(t)=-2t+10,
∴S′(1)=-2+10=8,
∴物体在1秒时的瞬时速度为8,
(2)f′(x)=-2x+10,
∴f′(1)=-2+10=8.
点评 本题考查了导数的物理意义,瞬时速度和平均速度,属于基础题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:解答题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
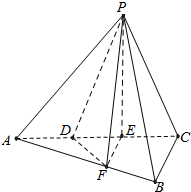 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com