考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,函数的性质及应用
分析:(1)利用函数单调性的定义可证明x>0时的单调性,根据奇函数性质可求x<0时f(x)的单调区间;
(2)对任意x1∈[1,3],总存在x2∈[1,3],使得g(x2)=h(x1)成立,等价于h(x)的值域为g(x)值域的子集,利用函数单调性易求两函数值域;
解答:
(1)证明:当x>0时,
①设x
1,x
2是区间
(0,]上的任意两个实数,且x
1<x
2,
则
f(x1)-f(x2)=(x1+)-(x2+)=
(x1-x2)+a()=(x
1-x
2)
•,
∵x
1,x
2∈
(0,],且x
1<x
2,
∴0<x
1x
2<a,x
1-x
2<0,x
1x
2>0,
∴f(x
1)-f(x
2)>0,即f(x
1)>f(x
2),
∴f(x)在
(0,]上是减函数,
②同理可证在f(x)在
[,+∞)上是增函数;
综上所述得:当x>0时,f(x)在
(0,]上是减函数,在
[,+∞)上是增函数.
∵函数
f(x)=x+(a>0)是奇函数,根据奇函数图象的性质可得,
当x<0时,f(x)在
[-,0)是减函数,在
(-∞,-]是增函数.
(2)解:∵
h(x)=x+-8(x∈[1,3]),
由(Ⅰ)知:h(x)在[1,2][1,3]上单调递减,[2,3]上单调递增,
∴h(x)
min=h(2)=-4,h(x)
max=maxh(3),h(1)=-3,
h(x)∈[-4,-3],
又∵g(x)在[1,3]上单调递减,
∴由题意知,[-4,-3]⊆[-3-2b,-1-2b],
于是有:
,解得
≤b≤1.
故实数b的范围是
≤b≤1.
点评:本题考查函数单调性的证明、应用,考查集合的简单运算,考查恒成立问题的求解,考查转化思想,考查学生分析解决问题的能力.



 快捷英语周周练系列答案
快捷英语周周练系列答案 小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示. 如图,在三棱锥A-BCD中,BA=BD,AD⊥CD,E、F分别为AC、AD的中点.
如图,在三棱锥A-BCD中,BA=BD,AD⊥CD,E、F分别为AC、AD的中点.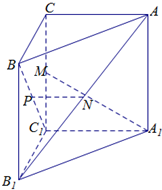 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=