
| 年份 | 2030 | 2035 | 2040 | 2045 | 2050 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 所占比例y | 68 | 65 | 62 | 62 | 61 |
分析 根据回归系数公式计算回归系数,得出回归方程.
解答 解:$\overline{t}$=$\frac{1+2+3+4+5}{5}=3$,$\overline{y}$=$\frac{68+65+62+62+61}{5}$=63.6.
$\sum_{i=1}^{5}({t}_{i}-\overline{t})({y}_{i}-\overline{y})$=(-2)×4.4+(-1)×1.4+0+1×(-1.6)+2×(-2.6)=-17.
$\sum_{i=1}^{5}({t}_{i}-\overline{t})^{2}$=4+1+0+1+2=10.
∴$\stackrel{∧}{b}$=-$\frac{17}{10}$=-1.7.$\stackrel{∧}{a}$=63.6+1.7×3=68.7.
∴y关于t的线性回归方程为y=-1.7t+68.7.
故答案为y=-1.7t+68.7.
点评 本题考查了线性回归方程的解法,属于基础题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
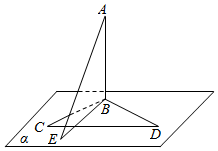 如图所示,在△BCD所在平面α内有一点E,BE=7cm,A为平面α外一点,AB⊥BC,AB⊥BD,且AB=5cm.
如图所示,在△BCD所在平面α内有一点E,BE=7cm,A为平面α外一点,AB⊥BC,AB⊥BD,且AB=5cm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com