
分析 (Ⅰ) 通过a=-5,不等式f(x)<1化为|x-2|-|x+5|<1,通过分类讨论求解不等式的解集即可.
(Ⅱ)通过x∈[1,2]时,化简不等式,利用解集的包含关系,列出与a有关的不等式求解即可.
解答 解:(Ⅰ) 当a=-5时,不等式f(x)<1化为|x-2|-|x+5|<1,
当x≤-5时,-(x-2)+(x+5)<1,无解;
当-5<x≤2时,-(x-2)-(x+5)<1,解得x>-2,又-5<x≤2,
所以-2<x≤2;
当x>2时,(x-2)-(x+5)≤1,恒成立,又x>2,所以x>2.
因此,当a=-5时,解不等式f(x)<1的解集为{x|x>-2}.
(Ⅱ) $f(x)≤-|{x-\frac{1}{4}}|$$?|{x-2}|-|{x-a}|+|{x-\frac{1}{4}}|≤0$.
当x∈[1,2]时,$-(x-2)-|{x-a}|+x-\frac{1}{4}≤0$,即$|{x-a}|≥\frac{7}{4}$,
所以$x≥a+\frac{7}{4}$或$x≤a-\frac{7}{4}$,
因为$f(x)≤-|{x-\frac{1}{4}}|$的解集包含[1,2],
于是$a+\frac{7}{4}≤1$或$a-\frac{7}{4}≥2$,故$a≤-\frac{3}{4}$或$a≥\frac{15}{4}$.
所以,实数a的取值范围为$(-∞,-\frac{3}{4}]∪[\frac{15}{4},+∞)$.
点评 本题考查绝对值不等式的解法,考查分类讨论以及转化思想的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
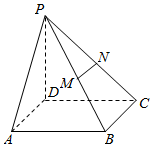 如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
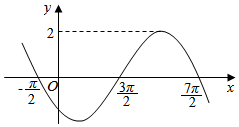
| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | -9 | C. | 7 | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com