
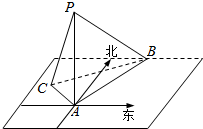
 如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.
如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时. 分析 在Rt△PAB、Rt△PAC中确定AB、AC的长,进而求得,∠CAB=20°+40°=60°,利用余弦定理求得BC,用里程除以时间即为船的速度.
解答 解:在Rt△PAB中,∠APB=30°,PA=$\sqrt{3}$,∴AB=1.
在Rt△PAC中,∠APC=60°,
∴AC=3.
在△ACB中,∠CAB=20°+40°=60°,
∴BC=$\sqrt{1+9-2×1×3×\frac{1}{2}}$=$\sqrt{7}$.
则船的航行速度$\sqrt{7}$÷$\frac{1}{6}$=$6\sqrt{7}$.
故答案为:$6\sqrt{7}$.
点评 本题主要考查考生运用数学知识解决实际问题的能力,考查学生的计算能力,比较基础.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤0} | B. | {x|1≤x≤2} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | $\frac{7}{4}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:| 未发病 | 发病 | 合计 | |
| 未注射疫苗 | 20 | x | A |
| 注射疫苗 | 30 | y | B |
| 合计 | 50 | 50 | 100 |
| P(X2≤K0) | 0.05 | 0.01 | 0.005 | 0.001 |
| K0 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,5] | B. | [4,6] | C. | (3,5) | D. | (4,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com