
分析 求出圆的标准方程,求出圆心和半径,根据直线和圆相切的等价条件进行求解即可.
解答 解:圆的标准方程为(x-1)2+(y-2)2=1,
则圆心为(1,2),半径R=1,
若切线斜率k不存在,即x=0时,满足条件.
若切线斜率k存在,则设切线方程为y=kx,
即kx-y=0,
圆心到直线的距离d=$\frac{|k-2|}{\sqrt{1+{k}^{2}}}$=1,
得|k-2|=$\sqrt{1+{k}^{2}}$,
平方得k2-4k+4=1+k2,
即k=$\frac{3}{4}$,此时切线方程为$y=\frac{3}{4}x$,
综上切线方程为:$y=\frac{3}{4}x$或x=0,
故答案为:$y=\frac{3}{4}x$或x=0.
点评 本题主要考查直线和圆位置关系的应用,根据直线和圆相切与半径之间的关系是解决本题的关键.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
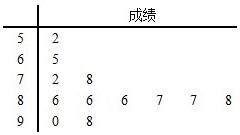 为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.
为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{7}$,+∞) | B. | [$\frac{1}{7}$,$\frac{1}{3}$) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{7}$]∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )
在四棱锥P-ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设$\frac{PE}{ED}$=m,则“0<m<2”是三棱锥C-ABE的体积不小于1的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com