考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的求值,三角函数的图像与性质
分析:(1)根据数量积的坐标运算化简f(x)=1-sin(2x+
),再由正弦函数性质可知,f(x)的单调递增区间为
(kπ+,kπ+),k∈Z;
(2)通过三角函数单调性直接求解即可;
(3)将2β分解成α+β-(α-β)然后利用两角差的余弦公式求解β,代入函数f(x)即可.
解答:
解:(1)∵向量
=(sin
2x+
,sinx)
=(sin
2x+cos
2x,sinx)
=(1,sinx),
=(
cos2x-
sin2x,2sinx),
∴f(x)=
•=
cos2x-
sin2x+2sin
2x
=1-
cos2x-
sin2x
=1-sin(2x+
),
由正弦函数性质可知,
f(x)的单调递增区间为
(kπ+,kπ+),k∈Z.
(2)由(1)知,
f(x)=1-sin(2x+
),
在x∈[0,
)时,f(x)为减函数,
∵当x=0时,x=
,
当x=
时,x=0.
∴f(x)的值域为
(0,].
(3)∵0<
α<β≤,
∴
<α-β<0,0<α+β<π
∴sin(α-β)<0,sin(α+β)>0.
∵cos(α-β)=
,cos(α+β)=-
,
sin(α-β)=-
,sin(α+β)=
.
∴cos2β=cos[(α+β)-(α-β)]
=cos(α+β)cos(α+β)+sin(α+β)sin(α-β)
=-1,
∴
β=.
∴
f()=1-sin(π+)=
.
点评:本题考查向量数量积运算,三角恒等变换公式,三角函数性质等知识的综合应用,属于中档题.



 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案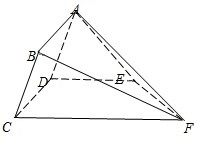 如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3
如图,矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角,DE∥CF,CD⊥DE,AD=2,EF=3