
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)﹣2tx在区间[﹣1,5]上是单调函数,求实数t的取值范围;
(3)若关于x的方程f(x)=x+m有区间(﹣1,2)上有唯一实数根,求实数m的取值范围(注:相等的实数根算一个).
【答案】
(1)解:设f(x)=ax2+bx+c(a≠0)
代入f(x+1)﹣f(x)=2x得2ax+a+b=2x对于x∈R恒成立,
故 ![]()
又由f(0)=1得c=1,
解得a=1,b=﹣1,c=1,
所以f(x)=x2﹣x+1
(2)解:因为g(x)=f(x)﹣2tx=x2﹣(2t+1)x+1的图象关于直线x= ![]() 对称,
对称,
又函数g(x)在[﹣1,5]上是单调函数,故 ![]() ≤﹣1或
≤﹣1或 ![]() ,
,
解得t≤ ![]() 或
或 ![]()
故实数t的取值范围是(﹣∞, ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
(3)解:由方程f(x)=x+m得x2﹣2x+1﹣m=0,
令h(x)=x2﹣2x+1﹣m,x∈(﹣1,2),即要求函数h(x)在(﹣1,2)上有唯一的零点,…(11分)
①若h(﹣1)=0,则m=4,代入原方程得x=﹣1或3,不合题意;
②若h(2)=0,则m=1,代入原方程得x=0或2,满足题意,故m=1成立;
③若△=0,则m=0,代入原方程得x=1,满足题意,故m=0成立;
④若m≠4且m≠1且m≠0时,由 ![]() 得1<m<4.
得1<m<4.
综上,实数m的取值范围是{0}∪[1,4)
【解析】(1)根据二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1,利用待定系数法,可得f(x)的解析式;(2)由g(x)=f(x)﹣2tx=x2﹣(2t+1)x+1的图象关于直线x= ![]() 对称,结合函数g(x)在[﹣1,5]上是单调函数,可得
对称,结合函数g(x)在[﹣1,5]上是单调函数,可得 ![]() ≤﹣1或
≤﹣1或 ![]() ,解得实数t的取值范围;(3)若关于x的方程f(x)=x+m有区间(﹣1,2)上有唯一实数根,则函数h(x)在(﹣1,2)上有唯一的零点,分类讨论,可得实数m的取值范围.
,解得实数t的取值范围;(3)若关于x的方程f(x)=x+m有区间(﹣1,2)上有唯一实数根,则函数h(x)在(﹣1,2)上有唯一的零点,分类讨论,可得实数m的取值范围.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】2017年“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图的频率分布直方图.
,后得到如图的频率分布直方图.
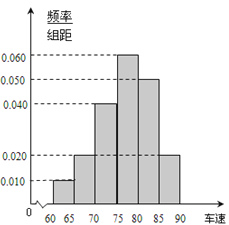
(1)求这40辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() ,
, ![]()
(1)求证:函数![]() 在点
在点![]() 处的切线恒过定点,并求出定点的坐标;
处的切线恒过定点,并求出定点的坐标;
(2)若![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,满足
上,满足![]() 恒成立的函数
恒成立的函数![]() 有无穷多个.(记
有无穷多个.(记![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,对任意实数m,n,都有f(m)f(n)=f(m+n),且当x<0时,0<f(x)<1.
(1)证明:①f(0)=1;②当x>0时,f(x)>1;③f(x)是R上的增函数;
(2)设a∈R,试解关于x的不等式f(x2﹣3ax+1)f(﹣3x+6a+1)≤1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(Ⅱ)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示. 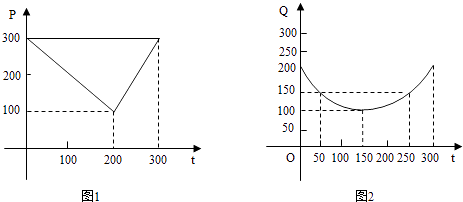
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com