
分析 根据函数的定义分别进行判断即可.
解答 解:①A={-1,0,1},B={-1,0,1},f:A中的数的平方;满足函数的定义,正确
②A={0,1},B={-1,0,1},f:A中的数的开方;不是函数关系,∵(±1)2=1,∴1有2个对应元素,不满足唯一性,不是函数关系.
③A=Z,B=Q,f:A中的数的倒数;不是函数关系,∵0的倒数不存在,∴0没有对应元素,不是函数关系.
④A=R,B={正实数},f:A中的数取绝对值;不是函数关系,∵0的绝对值是0,∴0没有对应元素,不是函数关系.
⑤A={1,2,3,4},B={2,4,6,8,10},f:n=2m,其中n∈A,m∈B;满足函数关系,
故答案为:2
点评 本题主要考查函数定义的判断,根据函数的定义是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{1}=1$ | D. | ${x^2}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
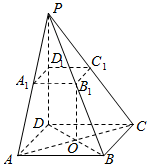 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{9\sqrt{3}}{4}$ | D. | $\frac{27\sqrt{3}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com