
分析 求出双曲线的渐近线,结合向量数量积的坐标关系,建立方程关系求出a,b,c即可得到结论.
解答 解:双曲线的渐近线方程为y=±$\frac{b}{a}$x,
不妨设其中一条渐近线为y=$\frac{b}{a}$x,右焦点为F(c,0)到渐近线y=$\frac{b}{a}$x的距离为|MF|=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
则$\overrightarrow{OF}$•$\overrightarrow{MF}$=|$\overrightarrow{OF}$|•|$\overrightarrow{MF}$|cos∠OFM=(|$\overrightarrow{OF}$|cos∠OFM)•|$\overrightarrow{MF}$|=|$\overrightarrow{MF}$||$\overrightarrow{MF}$|=b2=4,即b=2,
∵双曲线的离心率为$\frac{\sqrt{13}}{3}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{13}}{3}$,
即c2=$\frac{13}{9}$a2=a2+4,
得$\frac{4}{9}$a2=4,则a2=9,得a=3,c=$\sqrt{13}$,
故双曲线的方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}=1$,
故答案为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{4}=1$
点评 本题主要考查双曲线方程的求解,根据双曲线的离心率和向量的数量积建立方程关系求出a,b,c,的是解决本题的关键.


科目:高中数学 来源: 题型:选择题
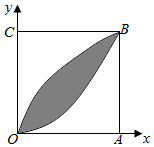 如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )
如图,在正方形OABC内.阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1),在正方形内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±4x | B. | y=±2x | C. | y=±$\frac{1}{2}x$ | D. | y=±$\frac{1}{4}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “f(0)=0”是“函数f(x)是奇函数”的充要条件 | |
| B. | “若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”的否命题是“若$α≠\frac{π}{6}$,则$sinα≠\frac{1}{2}$ | |
| C. | 若$p:?{x_0}∈R,x_0^2-{x_0}-1>0$,则¬p:?x∈R,x2-x-1<0 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com