
分析 利用给出的条件得出a=0,b的值,根据周期性和奇偶性得出(1)+f(2)+…+f(100)=f(1)=-f($\frac{1}{2}$)即可.
解答 解:∵定义在R上的函数f(x)是奇函数,
∴f(0)=0,
∵当$x∈[0,\frac{3}{4}]$时,$f(x)=\frac{a+sinπx}{{\sqrt{2}+cosπx}}-bx$(a、b∈R),
∴a=0,
即当$x∈[0,\frac{3}{4}]$时,f(x)=$\frac{sinπx}{\sqrt{2}+cosπx}$-bx(a、b∈R),
∵函数f(x)的周期为$\frac{3}{2}$,f(1)=f($\frac{3}{2}$$-\frac{1}{2}$)=f(-$\frac{1}{2}$),
f(2)=f($\frac{3}{2}$$+\frac{1}{2}$)=f($\frac{1}{2}$),
f(3)=f($\frac{3}{2}$+$\frac{3}{2}$)=f(0)=0
f(4)=f(3+1)=f(1)=f(-$\frac{1}{2}$),
…f(100)=f(99+1)=f(1)=f(-$\frac{1}{2}$)=-f($\frac{1}{2}$),
∴f(1)+f(2)+…+f(100)=f(1)=$-\frac{\sqrt{2}}{2}$$+\frac{b}{2}$,
∵定义在R上的函数f(x)既是奇函数,又是周期函数,且周期为$\frac{3}{2}$,
∴f(-$\frac{3}{4}$)=-f($\frac{3}{4}$)=-1+$\frac{3b}{4}$,
f(-$\frac{3}{4}$)=f($\frac{3}{2}$-$\frac{3}{4}$)=f($\frac{3}{4}$)=1-$\frac{3b}{4}$,
∴-1$+\frac{3b}{4}$=1-$\frac{3b}{4}$,求解b=$\frac{4}{3}$
∴f(1)+f(2)+…+f(100)=f(1)=-f($\frac{1}{2}$)=$-\frac{\sqrt{2}}{2}$$+\frac{b}{2}$=$-\frac{\sqrt{2}}{2}$$+\frac{2}{3}$,
故答案为:$-\frac{\sqrt{2}}{2}$$+\frac{2}{3}$.
点评 本题综合考查了函数的性质周期性运奇偶性的运用,整体运用的思想,考查了逻辑推理变换的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 10 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{2π}{3},\frac{4π}{3}]$ | B. | $[{\frac{5π}{6},2π}]$ | C. | $[{\frac{7π}{6},\frac{5π}{3}}]$ | D. | $[{\frac{7π}{6},2π}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
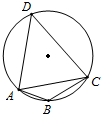 在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求:
在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com