
分析 根据重心性质可知:$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,代入a$\overrightarrow{GA}$+b$\overrightarrow{GB}$+$\frac{\sqrt{3}}{3}$c$\overrightarrow{GC}$=$\overrightarrow{0}$,得出a$\overrightarrow{GA}$+b$\overrightarrow{GB}$+$\frac{\sqrt{3}}{3}$c(-$\overrightarrow{GA}$$-\overrightarrow{GB}$)=$\overrightarrow{0}$,合并得出(a-$\frac{\sqrt{3}}{3}$c)$\overrightarrow{GA}$+(b$-\frac{\sqrt{3}}{3}$c)$\overrightarrow{GB}$=$\overrightarrow{0}$,
根据$\overrightarrow{GA}$,$\overrightarrow{GB}$不共线,系数同时为0求解a=b=$\frac{\sqrt{3}}{3}$c,利用余弦定理求解cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$即可.
解答 解:根据重心性质可知:$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,
∵a$\overrightarrow{GA}$+b$\overrightarrow{GB}$+$\frac{\sqrt{3}}{3}$c$\overrightarrow{GC}$=$\overrightarrow{0}$,
∴若a$\overrightarrow{GA}$+b$\overrightarrow{GB}$+$\frac{\sqrt{3}}{3}$c(-$\overrightarrow{GA}$$-\overrightarrow{GB}$)=$\overrightarrow{0}$,
∴若(a-$\frac{\sqrt{3}}{3}$c)$\overrightarrow{GA}$+(b$-\frac{\sqrt{3}}{3}$c)$\overrightarrow{GB}$=$\overrightarrow{0}$,
∵$\overrightarrow{GA}$,$\overrightarrow{GB}$不共线,
∴a=b=$\frac{\sqrt{3}}{3}$c,
∵cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\frac{1}{3}{c}^{2}+{c}^{2}-\frac{1}{3}{c}^{2}}{2×\frac{\sqrt{3}}{3}{c}^{2}}$=$\frac{\sqrt{3}}{2}$
∴A=30°,
故答案为:30°
点评 本题考查重心的性质和应用,是基础题.解题时要认真审题,注意余弦定理的灵活运用


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | -3.3 m/s | B. | 3.3 m/s | C. | -11.6 m/s | D. | 11.6 m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
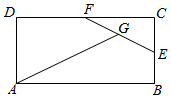 如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,
如图,在矩形ABCD中,AB=2AD,E,F分别为BC,CD的中点,G为EF中点,| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1] | B. | [-1,2) | C. | [-2,1] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com