
 棱长是1的正四面体PABC的四个顶点都在球O的表面上,若M、N分别是棱CA、CB的中点,则△PMN所在的平面截球O所得的截面面积是( )
棱长是1的正四面体PABC的四个顶点都在球O的表面上,若M、N分别是棱CA、CB的中点,则△PMN所在的平面截球O所得的截面面积是( )| A. | $\frac{2}{11}π$ | B. | $\frac{4}{11}π$ | C. | $\frac{8}{11}π$ | D. | $\frac{16}{11}π$ |
分析 由条件利用正四面体的性质,等边三角形的性质,三角形的重心的性质,求得球的半径PO的值,再利用等体积法求得点O到平面PMN的距离,可得平面PMN截球得到的截面圆的半径r的值,从而求得△PMN所在的平面截球O所得的截面面积.
解答 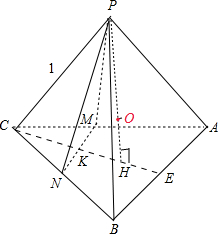 解:设等边△ABC的中心为H,球心为O,则PH⊥平面ABC,且O∈PH.
解:设等边△ABC的中心为H,球心为O,则PH⊥平面ABC,且O∈PH.
设CH∩MN=K,CH∩AB=E,则K为等腰三角形PMN的边MN的中点.
根据正四面体PABC的棱长为1,可得CE=$\frac{\sqrt{3}}{2}$×1=$\frac{\sqrt{3}}{2}$,CK=$\frac{1}{2}$CE=$\frac{\sqrt{3}}{4}$,CH=$\frac{2}{3}$CE=$\frac{\sqrt{3}}{3}$,
∴PH=$\sqrt{{PC}^{2}{-CH}^{2}}$=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$,HK=CH-CK=$\frac{\sqrt{3}}{12}$.
∵四面体ABCD的体积V=$\frac{1}{3}$•S△ABC•PH=4VO-ABC=4•$\frac{1}{3}$•S△ABC•OH,∴球的半径PO=$\frac{3}{4}$PH=$\frac{\sqrt{6}}{4}$.
设H到平面PMN的距离为x,则点O到平面PMN的距离为$\frac{3}{4}$x.
由VP-HMN=VH-PMN,可得$\frac{1}{3}$•($\frac{1}{2}$MN•HK)•PH=$\frac{1}{3}$•($\frac{1}{2}$•MN•PK)•x,可得HK•PH=PK•x,
即 $\frac{\sqrt{3}}{12}$×$\frac{\sqrt{6}}{3}$=$\sqrt{{PH}^{2}{+HK}^{2}}$x=$\sqrt{\frac{33}{48}}$•x,求得x=$\frac{\sqrt{2}}{3\sqrt{11}}$,∴点O到平面PMN的距离为$\frac{3}{4}$x=$\frac{\sqrt{2}}{4\sqrt{11}}$.
设平面PMN截球得到的截面圆的半径为r,则r=$\sqrt{{PO}^{2}{-(\frac{3}{4}x)}^{2}}$=$\frac{2\sqrt{11}}{11}$,故△PMN所在的平面截球O所得的截面面积为πr2=$\frac{4π}{11}$,
故选:B.
点评 本题主要考查正四面体的性质,用等体积法求出点到平面的距离,圆的截面性质,等边三角形的性质,三角形的重心的性质,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得e0≤0 | B. | sin2x+$\frac{2}{sinx}$≥3(x≠kπ,k∈Z) | ||
| C. | 函数f(x)=2x-x2有两个零点 | D. | a>1,b>1是ab>1的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com