
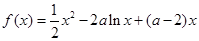 ,
,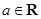 .
. 时,求函数
时,求函数 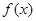 的最小值;
的最小值; 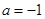 时,求证:无论
时,求证:无论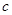 取何值,直线
取何值,直线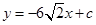 均不可能与函数
均不可能与函数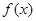 相切;
相切;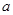 ,对任意的
,对任意的 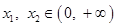 ,且
,且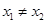 ,有
,有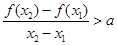 恒成立,若存在求出
恒成立,若存在求出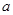 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。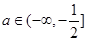 .
.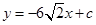 均不可能与函数f(x)相切;(3)假设存在实数a使得对任意的
均不可能与函数f(x)相切;(3)假设存在实数a使得对任意的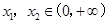 ,且
,且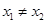 ,有
,有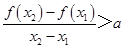 恒成立,假设
恒成立,假设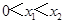 ,则
,则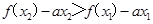 恒成立,构造辅助函数
恒成立,构造辅助函数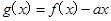 ,只要使函数g(x)在定义域内为增函数即可,利用其导函数恒大于等于0可求解a的取值范围.
,只要使函数g(x)在定义域内为增函数即可,利用其导函数恒大于等于0可求解a的取值范围.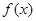 的定义域为
的定义域为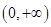 ,
, 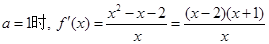 .
.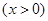
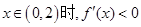 ,
,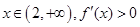 .
.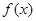 在
在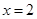 时取得最小值,其最小值为
时取得最小值,其最小值为 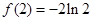 .
.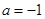
 ,
, 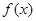 相切,设切点为
相切,设切点为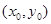 ,则
,则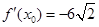
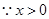
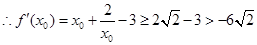 所以
所以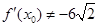 所以无论
所以无论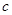 取何值,直线
取何值,直线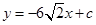 均不可能与函数
均不可能与函数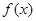 相切。
相切。 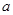 使得对任意的
使得对任意的 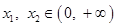 ,且
,且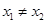 ,有
,有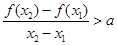 ,恒成立,不妨设
,恒成立,不妨设 ,只要
,只要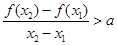 ,即:
,即: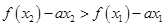
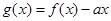 ,只要
,只要 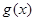 在
在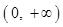 为增函数
为增函数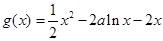 .
.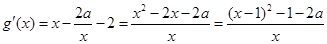
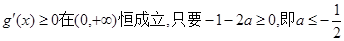 ,
,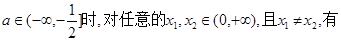
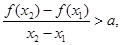 恒成立.
恒成立.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(0,1] | B.[1,+∞) |
| C.(-∞,-1]∪(0,1] | D.[-1,0)∪(0,1] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于 的近似函数关系式为
的近似函数关系式为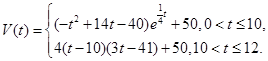
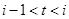 表示第1月份(
表示第1月份( ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?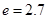 计算).
计算).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
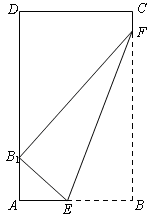
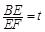 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为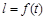 .
. 
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
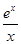 ,f(2)=
,f(2)=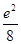 ,则x>0时,f(x)( )
,则x>0时,f(x)( )| A.有极大值,无极小值 |
| B.有极小值,无极大值 |
| C.既有极大值又有极小值 |
| D.既无极大值也无极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com