
分析 可作出图形:设河水的流速为$\overrightarrow{{V}_{1}}$,小船在静水中的速度为$\overrightarrow{{V}_{2}}$,船的实际速度为$\overrightarrow{V}$,根据题意便有$\overrightarrow{V}=\overrightarrow{{V}_{1}}+\overrightarrow{{V}_{2}}$,$|\overrightarrow{{V}_{1}}|=2,|\overrightarrow{V}|=10$,并且$\overrightarrow{V}⊥\overrightarrow{{V}_{1}}$,而$\overrightarrow{{V}_{2}}=\overrightarrow{V}-\overrightarrow{{V}_{1}}$,并可求出$(\overrightarrow{V}-\overrightarrow{{V}_{1}})^{2}$,从而便可求出$|\overrightarrow{{V}_{2}}|$,即求出小船在静水中的速度大小.
解答 解:解:设河水的流速为$\overrightarrow{{V}_{1}}$,小船在静水中的速度为$\overrightarrow{{V}_{2}}$,船的实际速度为$\overrightarrow{V}$,如图所示: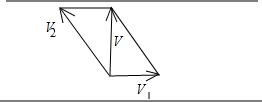 ,
,
则$\overrightarrow{V}=\overrightarrow{{V}_{1}}+\overrightarrow{{V}_{2}}$,$|\overrightarrow{{V}_{1}}|=2,|\overrightarrow{V}|=10$,且$\overrightarrow{V}⊥\overrightarrow{{V}_{1}}$;
∴$\overrightarrow{V}•\overrightarrow{{V}_{1}}=0$;
∴$|\overrightarrow{{V}_{2}}|=||\overrightarrow{V}-\overrightarrow{{V}_{1}}|$
=$\sqrt{{\overrightarrow{V}}^{2}-2\overrightarrow{V}•\overrightarrow{{V}_{1}}+{\overrightarrow{{V}_{1}}}^{2}}$
=$\sqrt{100-0+4}$
=$2\sqrt{26}$;
即小船在静水中的速度为$2\sqrt{26}$m/s.
点评 考查向量方法解决实际问题的方法,向量加法的平行四边形法则,向量的数乘运算,以及向量数量积的运算,向量垂直充要条件.


科目:高中数学 来源: 题型:选择题
| A. | ②③都不能为系统抽样 | B. | ②④都不能为分层抽样 | ||
| C. | ①④都可能为系统抽样 | D. | ①③都可能为分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D、E分别为棱CC1、B1C1的中点,
如图,直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D、E分别为棱CC1、B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
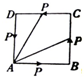 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
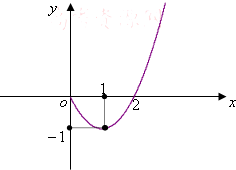 已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).
已知二次函数y=f(x)在[0,+∞)上的图象如图所示,顶点坐标为(1,-1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x±9y=0 | B. | 9x±4y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com