
在海岸A处,发现北偏东45°方向,距离A( -1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2n mile的C处的缉私船奉命以10
-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2n mile的C处的缉私船奉命以10 n mile/h的速度追截走私船.此时,走私船正以10n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
n mile/h的速度追截走私船.此时,走私船正以10n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
如图所示,注意到最快追上走私船且两船所用时间相等,若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求∠BCD. 
设缉私船用th在D处追上走私船,则有CD=10 t,BD=10t,
t,BD=10t,
在△ABC中,∵AB= -1,AC=2,∠BAC=120°,
-1,AC=2,∠BAC=120°,
∴由余弦定理得
BC2=AB2+AC2-2AB·AC·cos∠BAC
=( -1)2+22-2·(
-1)2+22-2·( -1)·2·cos120°=6,
-1)·2·cos120°=6,
∴BC=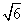 ,
,
∵cos∠CBA=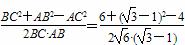 =
=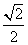 ,
,
∴∠CBA=45°,即B在C正东.
∵∠CBD=90°+30°=120°,
在△BCD中,由正弦定理得
sin∠BCD=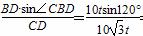 =
=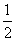 ,
,
∴∠BCD=30°.
即缉私船沿北偏东60°方向能最快追上走私船.


科目:高中数学 来源: 题型:
在△ABC中,角A,B,C所对的边分别为a,b,c,若b2+c2-a2= bc且b=
bc且b= a,则△ABC不可能是( )
a,则△ABC不可能是( )
A.等腰三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
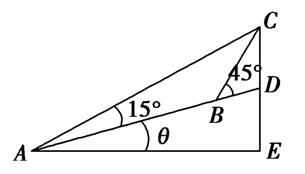
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=( )
A.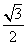 B.2-
B.2-
C. -1 D.
-1 D.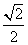
查看答案和解析>>
科目:高中数学 来源: 题型:
已知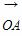 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),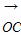 =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A、B、C能构成三角形,则实数m应满足的条件为________.
(2)若△ABC为Rt△,且∠A为直角,则m=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com