
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an).求证:
(1) 函数f(x)在区间(0,1)是增函数;
(2) an<an+1<1.
证明:(1) f(x)=x-xlnx,f′(x)=-lnx,当x∈(0,1)时,f′(x)=-lnx>0,故函数f(x)在区间(0,1)上是增函数.
(2) (用数学归纳法)①当n=1时,0<a1<1,a1ln a1<0,a2=f(a1)=a1-a1lna1>a1.
由函数f(x)在区间(0,1)是增函数,且f(1)=1,得f(x)在区间(0,1)是增函数,a2=f(a1)=a1-a1lna1<f(1)=1,即a1<a2<1成立.
②假设当n=k(k∈N*)时,ak<ak+1<1成立,
即0<a1≤ak≤ak+1<1,
那么当n=k+1时,由f(x)在区间(0,1]上是增函数,得0<a1≤ak≤ak+1<1,
得f(ak)<f(ak+1)<f(1),而an+1=f(an),则ak+1=f(ak),ak+2=f(ak+1),即ak+1<ak+2<1,也就是说当n=k+1时,an<an+1<1也成立.
由①②可得对任意的正整数n,an<an+1<1恒成立.


科目:高中数学 来源: 题型:
如图,F1、F2分别是双曲线C: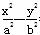 =1(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P、Q两点,线段PQ的垂直平分线与x轴交于点M.若MF2=F1F2,则C的离心率是________.
=1(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P、Q两点,线段PQ的垂直平分线与x轴交于点M.若MF2=F1F2,则C的离心率是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com