Question

13．已知定义在R上的奇函数f（x），满足f（x-2）=-f（x），且当x∈[0，1]时，f（x）=x²+x+sinx，若方程f（x）=m（m＞0）在区间[-4，4]上有四个不同的根x₁，x₂，x₃，x₄，则x₁+x₂+x₃+x₄的值为（　　）

• A． 2
• B． -2
• C． 4
• D． -4

Answer 1

分析 根据函数的条件，判断函数的周期，利用函数的奇偶性和周期性即可得到结论．

解答 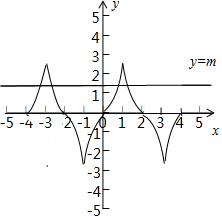解：∵f（x-2）=-f（x），
∴f（x-4）=-f（x-2）=f（x），
即函数的周期是4，
且f（x-2）=-f（x）=f（-x），
则函数的对称轴为：x=-1，f（x）是奇函数，
所以x=1也是对称轴，x∈[0，1]时，f（x）=x²+x+sinx，
函数是增函数，
作出函数f（x）的简图，
若方程f（x）=m（m＞0）在区间[-4，4]上
有四个不同的根x₁，x₂，x₃，x₄，
则四个根分别关于x=1和x=3对称，
不妨设x₁＜x₂＜x₃＜x₄，
则x₁+x₂=-6，x₃+x₄=2，
则x₁+x₂+x₃+x₄=-6+2=-4，
故选：D．

点评 本题主要考查方程根的应用，根据条件结合函数的周期性和奇偶性，利用数形结合是解决本题的关键．