
分析 (1)F(x)=x2+mx+1-ex,求其导函数,由题意可得F'(x)=2x+m-ex≥0对x∈[0,2]恒成立,即m≥ex-2x.令h(x)=ex-2x,x∈[0,2],利用导数求其最大值,则m的范围可求;
(2)$G(x)=\frac{f(x)}{g(x)}=\frac{{x}^{2}+mx+1}{{e}^{x}}$,$H(x)=-\frac{1}{4}x+\frac{5}{4}$.把不等式G(x)≤H(x)对x∈[0,5]恒成立转化为${x^2}+mx+1≤{e^x}(-\frac{1}{4}x+\frac{5}{4})$对x∈[0,5]恒成立,令φ(x)=${e}^{x}(-\frac{1}{4}x+\frac{5}{4})$,利用导数求其单调性,作出φ(x)的大致图象,数形结合可得答案.
解答 解:(1)∵f(x)=x2+mx+1,g(x)=ex,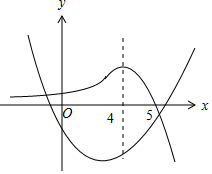
∴F(x)=x2+mx+1-ex,得F'(x)=2x+m-ex.
又∵x∈[0,2]时F(x)为增函数,∴F'(x)=2x+m-ex≥0对x∈[0,2]恒成立,即m≥ex-2x.
令h(x)=ex-2x,x∈[0,2],则h'(x)=ex-2,由h'(x)=0,解得x=ln2.
当x∈(0,ln2)时,h'(x)<0,当x∈(ln2,2)时,h'(x)>0,
∴h(x)在[0,ln2]单调递减;在(ln2,2]单调递增,
又∵h(0)=1,h(2)=e2-4>1,
∴$h{(x)_{max}}=h(2)={e^2}-4$,
∴m≥e2-4;
(2)$G(x)=\frac{f(x)}{g(x)}=\frac{{x}^{2}+mx+1}{{e}^{x}}$,$H(x)=-\frac{1}{4}x+\frac{5}{4}$.
不等式G(x)≤H(x)对x∈[0,5]恒成立,即${x^2}+mx+1≤{e^x}(-\frac{1}{4}x+\frac{5}{4})$对x∈[0,5]恒成立,
令φ(x)=${e}^{x}(-\frac{1}{4}x+\frac{5}{4})$,则φ′(x)=${e}^{x}(-\frac{1}{4}x+1)$,
令φ'(x)=0,得x=4,
当x∈(-∞,4)时,φ′(x)>0,当x∈(4,+∞)时,φ′(x)<0,
∴φ(x)在(-∞,4)单调递增;在(4,+∞)上单调递减,
又∵φ(x)=0有唯一零点x=5,作出函数φ(x)的图象如图:
∵当x=0时,x2+mx+1=1<${e}^{0}(-\frac{1}{4}×0+\frac{5}{4})=\frac{5}{4}$成立.
∴要满足r(x)=x2+mx+1≤φ(x)对x∈[0,5]恒成立,
只需r(5)≤0,即26+5m≤0,解得$m≤-\frac{26}{5}$.
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的最值,体现了数学转化思想方法和数形结合的解题思想方法,属难题.


科目:高中数学 来源: 题型:选择题
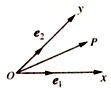 如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )
如图,设Ox、Oy是平面内相交成45°角的两条数轴,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$分别是x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$,则把有序数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标,在此坐标系下,假设$\overrightarrow{OA}$=(-2,2$\sqrt{2}$),$\overrightarrow{OB}$=(2,0),$\overrightarrow{OC}$=(5,-3$\sqrt{2}$),则下列命题不正确的是( )| A. | $\overrightarrow{{e}_{1}}$=(1,0) | B. | |$\overrightarrow{OA}$|=2$\sqrt{3}$ | C. | $\overrightarrow{OA}$∥$\overrightarrow{BC}$ | D. | $\overrightarrow{OA}$⊥$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | 3 | C. | $\frac{\sqrt{10}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}-\frac{4π}{3}$ | B. | $2\sqrt{3}-\frac{2π}{3}$ | C. | $2\sqrt{3}+\frac{4π}{3}$ | D. | $2\sqrt{3}+\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | B. | $\frac{5}{4}$或5 | C. | 5 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com