
分析 (1)利用等差数列的性质求出首项和公差,再代入通项公式和求和公式即可;
(2)bn=$\frac{1}{{{a_n}^2-4}}$═$\frac{1}{({a}_{n}+2)({a}_{n}-2)}$,使用裂项法数列求和.
解答 解:(I)∵{an}为等差数列,∴2a6=a5+a7=26,即a6=13,
∴3d=a6-a3=6,即d=2,
∴a1=a3-2d=3,
∴an=3+2(n-1)=2n+1,
Sn=na1+$\frac{n(n-1)}{2}d$=n2+2n.
(II)bn=$\frac{1}{({a}_{n}+2)({a}_{n}-2)}$=$\frac{1}{(2n+3)(2n-1)}$=$\frac{1}{4}$($\frac{1}{2n-1}-\frac{1}{2n+3}$).
∴Tn=$\frac{1}{4}$(1-$\frac{1}{5}$)+$\frac{1}{4}$($\frac{1}{3}-\frac{1}{7}$)+$\frac{1}{4}$($\frac{1}{5}-\frac{1}{9}$)+…+$\frac{1}{4}$($\frac{1}{2n-3}$-$\frac{1}{2n+1}$)+$\frac{1}{4}$($\frac{1}{2n-1}-\frac{1}{2n+3}$)
=$\frac{1}{4}$(1-$\frac{1}{5}$+$\frac{1}{3}-\frac{1}{7}$+$\frac{1}{5}-\frac{1}{9}$+…+$\frac{1}{2n-3}$-$\frac{1}{2n+1}$+$\frac{1}{2n-1}-\frac{1}{2n+3}$)
=$\frac{1}{4}$(1+$\frac{1}{3}$-$\frac{1}{2n+1}$-$\frac{1}{2n+3}$)
=$\frac{1}{3}$-$\frac{1}{4(2n+1)}$-$\frac{1}{4(2n+3)}$.
点评 本题考查了等差数列的性质,裂项法数列求和,属于中档题.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
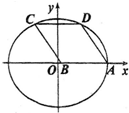 已知圆F的方程为x2+y2-2x=0,与x轴正半轴交于点A,椭圆C的中心在原点,焦点在圆心F,顶点为A.
已知圆F的方程为x2+y2-2x=0,与x轴正半轴交于点A,椭圆C的中心在原点,焦点在圆心F,顶点为A.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | 1-$\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | 1-$\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{1}{4}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
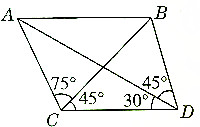 如图,在四边形ABDC中,CD=$\sqrt{3}$,∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求AB的长.
如图,在四边形ABDC中,CD=$\sqrt{3}$,∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求AB的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com