
分析 利用导数判断函数的单调性,求出函数的定义域,利用函数的导数通过恒成立,转化求解即可.
解答 解:因为$\frac{{f({x_1}+1)-f({x_2}+1)}}{{{x_1}-{x_2}}}$表示点(x1+1,f(x1+1))与点(x2+1,f(x2+1))连线的斜率,
因为x1,x2∈(0,1)且x1≠x2,不等式$\frac{{f({x_1}+1)-f({x_2}+1)}}{{{x_1}-{x_2}}}>1$恒成立,
所以函数图象在区间(1,2)内任意两点连线的斜率大于1,
即函数的导数大于1在(1,2)内恒成立,由函数的定义域知,x>-1,
所以f'(x)=$\frac{a}{x+1}-2x>1$在(1,2)内恒成立,即a>2x2+3x+1在(1,2)内恒成立,
即a大于或等于2x2+3x+1在[1,2]上的最大值,
由二次函数的性质知,y=2x2+3x+1在[1,2]上是单调增函数,
故x=2时,y=2x2+3x+1在[1,2]上取最大值为15,故a>15.
故答案为:a≥15.
点评 本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,二次函数的性质的应用,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )
如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )| A. | 重心 | B. | 垂心 | C. | 内心 | D. | 外心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
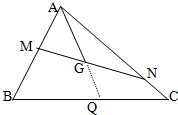 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 12 | C. | 9 | D. | 与k的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
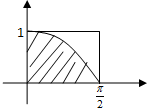

| A. | 60 | B. | 62 | C. | 64 | D. | 66 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
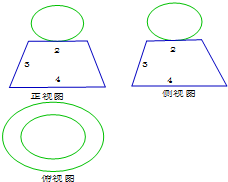
| A. | $\frac{π}{3}(4+14\sqrt{2})$ | B. | $\frac{{14\sqrt{2}π}}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{4π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com