
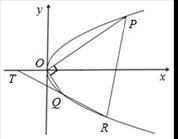
设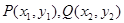 是抛物线
是抛物线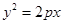
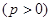 上相异两点,
上相异两点, 到y轴的距离的积为
到y轴的距离的积为 且
且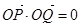 .
.
(1)求该抛物线的标准方程.
(2)过Q的直线与抛物线的另一交点为R,与 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
(1)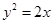 .(2)直线PQ垂直于x轴时|PR|取最小值
.(2)直线PQ垂直于x轴时|PR|取最小值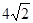 .
.
解析试题分析:(1)确定抛物线的标准方程,关键是确定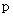 的值.利用
的值.利用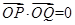 ,可得
,可得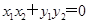 ,
,
再根据P、Q在抛物线上,得到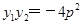 ,集合已知条件
,集合已知条件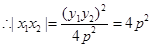 ,得4p2=4,p=1.
,得4p2=4,p=1.
(2)设直线PQ过点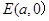 ,且方程为
,且方程为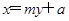 ,应用联立方程组
,应用联立方程组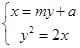
消去x得y2 2my 2a=0,利用韦达定理,建立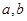 的方程组,确定
的方程组,确定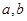 得到
得到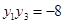 ,利用“弦长公式”求解.
,利用“弦长公式”求解.
试题解析: (1)∵ ·=0,则x1x2+y1y2=0, 1分
又P、Q在抛物线上,故y12=2px1,y22=2px2,故得
+y1y2=0, y1y2= 4p2 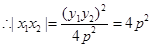 3分
3分
又|x1x2|=4,故得4p2=4,p=1.
所以抛物线的方程为: 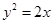 5分
5分
(2)设直线PQ过点E(a,0)且方程为x=my+a
联立方程组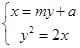
消去x得y2 2my 2a=0
∴ 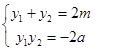 ① 7分
① 7分
设直线PR与x轴交于点M(b,0),则可设直线PR方程为x=ny+b,并设R(x3,y3),
同理可知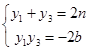 ② 9分
② 9分
由①、②可得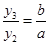
由题意,Q为线段RT的中点,∴ y3=2y2,∴b=2a
又由(Ⅰ)知, y1y2= 4,代入①,可得
2a= 4 ∴ a=2.故b=4. 11分
∴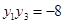
∴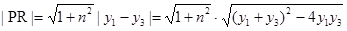
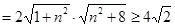 .
.
当n=0,即直线PQ垂直于x轴时|PR|取最小值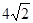 14分
14分
考点:抛物线标准方程,直线与抛物线的位置关系.


科目:高中数学 来源: 题型:解答题
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板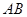 长为2m,跳水板距水面
长为2m,跳水板距水面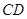 的高
的高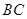 为3m,
为3m, =5m,
=5m,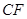 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点 m(
m(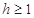 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以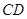 为横轴,
为横轴,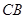 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.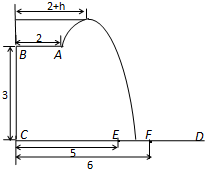
(1)当 =1时,求跳水曲线所在的抛物线方程;
=1时,求跳水曲线所在的抛物线方程;
(2)若跳水运动员在区域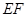 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系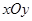 中,已知点
中,已知点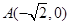 ,
,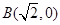 ,
,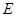 为动点,且直线
为动点,且直线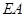 与直线
与直线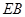 的斜率之积为
的斜率之积为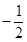 .
.
(1)求动点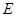 的轨迹
的轨迹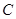 的方程;
的方程;
(2)设过点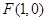 的直线
的直线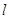 与曲线
与曲线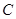 相交于不同的两点
相交于不同的两点 ,
, .若点
.若点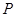 在
在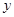 轴上,且
轴上,且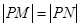 ,求点
,求点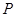 的纵坐标的取值范围.
的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设椭圆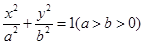 的左焦点为
的左焦点为 ,离心率为
,离心率为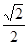 ,过点
,过点 且与
且与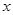 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为 .
.
(1) 求椭圆方程.
(2) 过点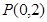 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点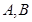 ,当
,当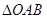 面积最大时,求
面积最大时,求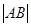 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,F1,F2是离心率为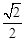 的椭圆C:
的椭圆C: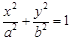 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线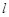 :x=-
:x=-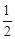 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.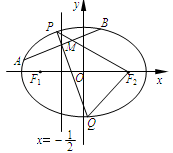
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 求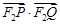 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知在直角坐标系 中,曲线
中,曲线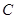 的参数方程为:
的参数方程为: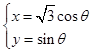 (
(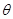 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线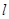 的极坐标方程为:
的极坐标方程为: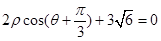 .
.
(Ⅰ)写出曲线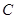 和直线
和直线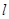 在直角坐标系下的方程;
在直角坐标系下的方程;
(II)设点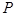 是曲线
是曲线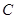 上的一个动点,求它到直线
上的一个动点,求它到直线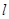 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com