练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．有个小偷在警察面前作了如下辩解：是我的录像机，我就一定能把它打开．看，我把它打开了．所以它是我的录像机．请问这一推理错在（　　）
    A．大前提B．小前提C．结论D．以上都不是

    分析 本题考查的知识点是演绎推理的基本方法及整数的分类，在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是推理形式错误，我们分析的其大前提的形式：“是我的录像机，我就一定能把它打开”，不难得到结论．

    解答 解：∵大前提的形式：“是我的录像机，我就一定能把它打开”错误；
    故此推理错误原因为：大前提错误，
    故选：A

    点评 演绎推理是一种必然性推理，演绎推理的前提与结论之间有蕴涵关系．因而，只要前提是真实的，推理的形式是正确的，那么结论必定是真实的，但错误的前提可能导致错误的结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+3ax+{a}^{2}-3，（x＜0）}\\{2{e}^{x}-（x-a）^{2}+3，（x＞0）}\end{array}\right.$，a∈R．
    （Ⅰ）若函数y=f（x）在x=1处取得极值，求a的值；
    （Ⅱ）若函数y=f（x）的图象上存在两点关于原点对称，求a的范围；
    （Ⅲ）当x≥2时，记g（x）=f（x）+（x-a）2+（a-x）3-3+6ex，若g（x）≥0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．若ab＜0且a+b=1，二项式（a+b）9按a的降幂排列，展开后其第二项不大于第三项，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知i是虚数单位，则（$\frac{1+i}{{\sqrt{2}}}$）2015在复平面内对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，$\overrightarrow{CA}$=$\vec a$，$\overrightarrow{CB}$=$\vec b$，D、E分别是CA、CB的中点，$\overrightarrow{DE}$=（　　）
    A．$\vec a$-$\vec b$B．$\vec b$-$\vec a$C．$\frac{1}{2}$（$\vec a$-$\vec b$）D．$\frac{1}{2}$（$\vec b$-$\vec a$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知△ABC中，a=4$\sqrt{3}$，b=4，A=60°，则B等于（　　）
    A．30°B．30°或150°C．60°D．60°或120°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

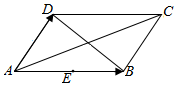
    12．在平行四边形ABCD中，E为AB的中点，$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$，则下列向量表示错误的是（　　）
    A．$\overrightarrow{AC}$=$\overrightarrow a$+$\overrightarrow b$B．$\overrightarrow{BD}$=$\overrightarrow a$-$\overrightarrow b$C．$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow a$D．$\overrightarrow{CB}$=-$\overrightarrow b$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设集合P={x|0≤x≤3}，N={x∈Z|-3＜x＜3}，则P∩N=（　　）
    A．{x|0≤x＜3}B．{x|-3＜x＜3}C．{0，1，2}D．{0，1，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．10名同学在高一和高二的数学成绩如表（百分制）：
    x74716876736770657472
    y76757076796577627271
    其中x为高一数学成绩，y为高二数学成绩．
    （1）作出散点图并判断y与x是否是相关关系，如果是，求回归直线方程．
    （2）若某同学高一的数学成绩是80分，那么他高二的数学成绩约为多少？
    （附：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\stackrel{-2}{x}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，其中$\overline{x}$，$\overline{y}$为样本平均值）
    $\sum_{i=1}^{10}{x}_{i}$=710，$\sum_{i=1}^{10}{y}_{i}$=723，$\overline{x}$=71，$\overline{y}$=72.3，$\sum_{i=1}^{10}{x}_{i}{y}_{i}$=51476，$\sum_{i=1}^{10}{{x}_{1}}^{2}$=50520，$\sum_{i=1}^{10}{{y}_{1}}^{2}$=52541．

    查看答案和解析>>

    同步练习册答案