
分析 (Ⅰ)设椭圆E的方程为$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$,通过离心率$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,以及a,b,c的关系,利用以椭圆E的长轴和短轴为对角线的四边形的周长为$4\sqrt{5}$,求出a,b,即可得到椭圆E的方程.
(Ⅱ) 求出P(0,m),设A(x1,kx1+m),B(x2,kx2+m),通过直线与椭圆方程联立,利用△>0,推出不等式,k2-m2+4>0.由$\overrightarrow{AP}=3\overrightarrow{PB}$,得到${k^2}=\frac{{4-{m^2}}}{{{m^2}-1}}$,然后求解m2的取值范围.
解答 解:(Ⅰ)根据已知设椭圆E的方程为$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$,焦距为2c,由已知得$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,
∴$c=\frac{{\sqrt{3}}}{2}a,{b^2}={a^2}-{c^2}=\frac{a^2}{4}$.…(3分)
∵以椭圆E的长轴和短轴为对角线的四边形的周长为$4\sqrt{5}$,∴$4\sqrt{{a^2}+{b^2}}=2\sqrt{5}a=4\sqrt{5}$,
∴a=2,b=1.
∴椭圆E的方程为${x^2}+\frac{y^2}{4}=1$.…(6分)
(Ⅱ) 根据已知得P(0,m),设A(x1,kx1+m),B(x2,kx2+m),
由$\left\{\begin{array}{l}y=kx+m\\ 4{x^2}+{y^2}-4=0\end{array}\right.$得(k2+4)x2+2mkx+m2-4=0,
由已知得△=4m2k2-4(k2+4)(m2-4)>0,
即k2-m2+4>0.且${x_1}+{x_2}=\frac{-2km}{{{k^2}+4}},{x_1}{x_2}=\frac{{{m^2}-4}}{{{k^2}+4}}$.…(9分)
由$\overrightarrow{AP}=3\overrightarrow{PB}$得-x1=3x2,即x1=-3x2.
∴$3{({{x_1}+{x_2}})^2}+4{x_1}{x_2}=0$,
∴$\frac{{12{k^2}{m^2}}}{{{{({{k^2}+4})}^2}}}+\frac{{4({{m^2}-4})}}{{{k^2}+4}}=0$,即m2k2+m2-k2-4=0.当m2=1时,m2k2+m2-k2-4=0不成立.
∴${k^2}=\frac{{4-{m^2}}}{{{m^2}-1}}$,∵k2-m2+4>0,∴$\frac{{4-{m^2}}}{{{m^2}-1}}-{m^2}+4>0$,即$\frac{{({4-{m^2}}){m^2}}}{{{m^2}-1}}>0$.
∴1<m2<4,
所以m2的取值范围为(1,4).…(12分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查分析问题解决问题的能力,转化思想的应用.


科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
若一个四棱锥底面为正方形, 顶点在底面的射影为正方形的中心, 且该四棱锥的体积为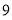 ,当其外接球的体积最小时, 它的高为( )
,当其外接球的体积最小时, 它的高为( )
A.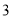 B.
B.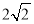 C.
C.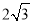 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
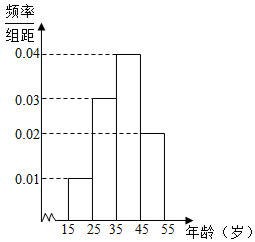 某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
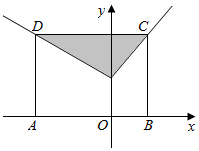 如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,ABCD为矩形,C、D两点在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,点A、B在x轴上,且B(1,0),若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 营养成分 | 碳水化合物/单位 | 蛋白质/单位 | 维生素C/单位 |
| 午餐 | |||
| 晚餐 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com