
分析 (1)由题意可知:当n=1时,a1=1.当n≥2时,a1+2a2+…+nan=4-$\frac{n+2}{{2}^{n-1}}$,a1+2a2+…+(n-1)an-1=4-$\frac{n+1}{{2}^{n-2}}$,两式相减即可求得数列{an}的通项公式;
(2)由bn=(3n-2)$\frac{1}{{2}^{n-1}}$,采用“错位相减法”即可求得数列{bn}的前n项和Sn.
解答 解:(1)当n=1时,a1=4-$\frac{3}{{2}^{0}}$=1.
当n≥2时,a1+2a2+…+nan=4-$\frac{n+2}{{2}^{n-1}}$…①
a1+2a2+…+(n-1)an-1=4-$\frac{n+1}{{2}^{n-2}}$…②
①-②得:nan=$\frac{n+1}{{2}^{n-2}}$-$\frac{n+2}{{2}^{n-1}}$=$\frac{1}{{2}^{n-1}}$(2n+2-n-2)=$\frac{n}{{2}^{n-1}}$
∴an=$\frac{1}{{2}^{n-1}}$,
当n=1时,a1也适合上式,
∴数列{an}的通项公式an=$\frac{1}{{2}^{n-1}}$ (n∈N*).
(2)bn=(3n-2)$\frac{1}{{2}^{n-1}}$,
Sn=$\frac{1}{{2}^{0}}$+$\frac{4}{{2}^{1}}$+$\frac{7}{{2}^{2}}$+…+(3n-5)$\frac{1}{{2}^{n-2}}$+(3n-2)$\frac{1}{{2}^{n-1}}$,…①
$\frac{1}{2}$Sn=$\frac{1}{{2}^{1}}$+$\frac{4}{{2}^{2}}$+$\frac{7}{{2}^{3}}$+…+(3n-5)$\frac{1}{{2}^{n-1}}$+(3n-2)$\frac{1}{{2}^{n}}$,…②
①-②得:$\frac{1}{2}$Sn=1+3($\frac{1}{{2}^{1}}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$ )-(3n-2)$\frac{1}{{2}^{n}}$
=1+3•$\frac{\frac{1}{2}-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-(3n-2)$\frac{1}{{2}^{n}}$=4-$\frac{3n+4}{{2}^{n}}$,
∴Sn=8-$\frac{3n+4}{{2}^{n-1}}$.
∴数列{bn}的前n项和Sn,Sn=8-$\frac{3n+4}{{2}^{n-1}}$.
点评 本题考查数列的递推公式,等比数列前n项和公式,“错位相减法”求数列的前n项和,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2016,2017) | B. | (2016,2017] | C. | [2016,2017) | D. | (-2016,2017) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞同 | 4 | 5 | 12 | 8 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
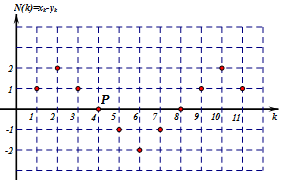 已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.
已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com