
| A. | (1,$\sqrt{2}$] | B. | [1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$-1] | D. | [1,$\sqrt{2}$-1] |
分析 由题意和勾股定理列出方程,利用完全平方公式表示出a+b,利用面积相等求出内切圆的半径r,根据换元法和基本不等式求出r的取值范围.
解答 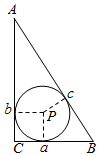 解:设AC=b、BC=a,且AB=2,C=90°,
解:设AC=b、BC=a,且AB=2,C=90°,
∴a2+b2=4,
∴(a+b)2=a2+b2+2ab=4+2ab,
则a+b=$\sqrt{4+2ab}$,
由$\frac{1}{2}ab=\frac{1}{2}(a+b+2)r$得,r=$\frac{ab}{a+b+2}$,
∴r=$\frac{ab}{\sqrt{4+2ab}+2}$,
设t=$\sqrt{4+2ab}$,则ab=$\frac{{t}^{2}-4}{2}$,
由a2+b2=4且a2+b2≥2ab得,0<ab≤2,当且仅当a=b时取等号,
∴4<4+2ab≤8,则2 $<\sqrt{4+2ab}≤2\sqrt{2}$,即t$∈(2,2\sqrt{2}]$,
代入r=$\frac{ab}{\sqrt{4+2ab}+2}$得,y=$\frac{\frac{{t}^{2}-4}{2}}{t+2}$=$\frac{1}{2}(t-2)$,
∵t$∈(2,2\sqrt{2}]$,∴$0<\frac{1}{2}(t-2)≤\sqrt{2}-1$,
∴其内切圆的半径r的取值范围(0,$\sqrt{2}-1$],
故选:C.
点评 本题考查了三角形内切圆的问题,基本不等式在最值问题中的应用,以及换元法、等面积法,考查化简、变形能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$ln2,+∞) | B. | [0,$\frac{1}{3}$ln2] | C. | (-∞,0] | D. | (-∞,$\frac{1}{3}$ln2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {1} | C. | {1,2,} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2014}$-1 | B. | $\sqrt{2015}$-1 | C. | $\sqrt{2016}$-1 | D. | $\sqrt{2016}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{6}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a>b>c | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com