
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | $\sqrt{5}$ | D�� | 2 |
���� �������⣬��˫���ߵ���ΪF1�������ɵ�PF1��PF��|PF1|=b��|PF|=2a+b���ɴ˿ɵ�b=2a����˫���ߵļ������ʿɵ���c=$\sqrt{5}$a�����˫���ߵ������ʹ�ʽ����ɵô𰸣�
��� �⣺�������⣬��˫���ߵ���ΪF1������F1��
��Բ��Բ��ΪC��Բ�ķ���Ϊ��x-$\frac{c}{3}$��2+y2=$\frac{{b}^{2}}{9}$��Բ��Ϊ��$\frac{c}{3}$��0�����뾶r=$\frac{b}{3}$��
����|F1F|=3|FC|��
��$\overrightarrow{PQ}$=2$\overrightarrow{QF}$����PF1��QC��|PF1|=b��|PF|=2a+b��
�߶�PF��Բ��x-$\frac{c}{3}$��2+y2=$\frac{{b}^{2}}{9}$�����ڵ�Q����CQ��PF�Լ�PF1��PF��
����b2+��2a+b��2=4c2��
��b2+��2a+b��2=4��a2+b2����
��b=2a��
��˫���ߵ�������c=$\sqrt{5}$a��
��˫���ߵ�������e=$\frac{c}{a}$=$\sqrt{5}$��
��ѡ��C��
���� ���⿼��˫���ߵļ������ʣ��漰ֱ����Բ��λ�ù�ϵ���ؼ��Ƿ���˫���ߡ�ֱ����Բ�Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | e2x | B�� | e2x-1 | C�� | e2x-2 | D�� | e2x-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
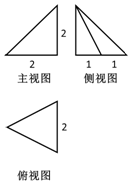
| A�� | $\frac{4}{3}$ | B�� | $7+\sqrt{5}$ | C�� | $5+\sqrt{5}$ | D�� | $7+2\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | i��5 | B�� | i��6 | C�� | i��4 | D�� | i��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 7 | C�� | 14 | D�� | 21 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
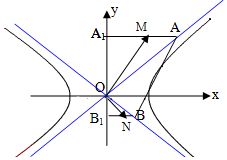 ��ͼ��A��B�ֱ���˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$���������ϵĵ㣬A��B��y���ϵ���Ӱ�ֱ�ΪA1��B1��M��N�ֱ���A1A��B1B�����е㣬��AB�е���˫�����ϣ���$\overrightarrow{OM}•\overrightarrow{ON}��-{a^2}$����˫���ߵ������ʵ�ȡֵ��ΧΪ��������
��ͼ��A��B�ֱ���˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$���������ϵĵ㣬A��B��y���ϵ���Ӱ�ֱ�ΪA1��B1��M��N�ֱ���A1A��B1B�����е㣬��AB�е���˫�����ϣ���$\overrightarrow{OM}•\overrightarrow{ON}��-{a^2}$����˫���ߵ������ʵ�ȡֵ��ΧΪ��������| A�� | $��{1��\frac{3}{2}}]$ | B�� | $[\frac{3}{2}��+�ޣ�$ | C�� | $��1��\frac{{\sqrt{5}}}{2}]$ | D�� | $[\frac{{\sqrt{5}}}{2}��+�ޣ�$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 2017��5�£�ӡ�ȵ�Ӱ��ˤ�Ӱɣ��ְ֡����й���ӳ��Ϊ���˽��������ڵ�����ȣ�ijӰԺ��������˱��йۿ�ӰƬ�Ĺ��ڣ��ִӵ�����Ⱥ�������ȡ13����������ͼ��ʾ�ľ�Ҷͼ��¼�����ǵ�����ȷ�����10���ƣ�����С����ǰ��һλ����Ϊ����С������һλ����ΪҶ����������������9�֣���Ƹù���Ϊ��������ڡ���
2017��5�£�ӡ�ȵ�Ӱ��ˤ�Ӱɣ��ְ֡����й���ӳ��Ϊ���˽��������ڵ�����ȣ�ijӰԺ��������˱��йۿ�ӰƬ�Ĺ��ڣ��ִӵ�����Ⱥ�������ȡ13����������ͼ��ʾ�ľ�Ҷͼ��¼�����ǵ�����ȷ�����10���ƣ�����С����ǰ��һλ����Ϊ����С������һλ����ΪҶ����������������9�֣���Ƹù���Ϊ��������ڡ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com