
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由题意可得函数f(x)的图象关于点M(1,0)对称,又关于直线x=-1对称;再结合g(x)的解析式画出这2个函数区间[-3,3]上的图象,数形结合可得它们的图象区间[-3,3]上的交点个数.
解答 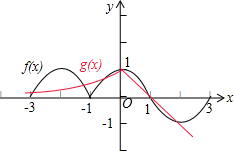 解:由f(x)+f(2-x)=0,可得函数f(x)的图象
解:由f(x)+f(2-x)=0,可得函数f(x)的图象
关于点M(1,0)对称.
由f(x-2)=f(-x),可得函数f(x)的图象
关于直线x=-1对称.
又f(x)在[-1,1]上表达式为
f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[-1,0]\\ cos(\frac{π}{2}x),x∈(0,1]\end{array}$,
可得函数f(x)在[-3,3]上的图象以及函数g(x)=$\left\{\begin{array}{l}{{2}^{x},x≤0}\\{1-x,x>0}\end{array}\right.$在[-3,3]上的图象,
数形结合可得函数f(x)的图象与函数g(x)的图象区间[-3,3]上的交点个数为6,
故选:B.
点评 本题主要考查函数的图象的对称性,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 7$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
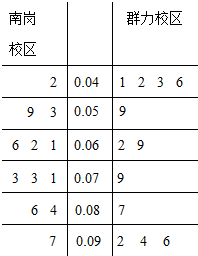 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )| A. | 南岗校区 | B. | 群力校区 | ||
| C. | 南岗、群力两个校区相等 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com