
分析 化简集合A,根据A∪B=A,建立条件关系,根据集合的基本运算即可求求由实数n所构成的集合N.
解答 解:依题意得A={x|x2-3x-4=0}={-1,4},
∵A∪B=A,
∴B⊆A,所以集合B可分为{1},{-4},或∅.
①当B=φ时,即方程nx+1=0无实根,所以n=0,符合题意;
②当B={-1}时,有-1是方程nx+1=0的根,所以n=1,符合题意;
③当B={4}时,有4是方程nx+1=0的根,所以$n=-\frac{1}{4}$,符合题意;
综上所得,a=0或a=1或$a=-\frac{1}{4}$.所以构成的集合$N=\left\{{0,1,-\frac{1}{4}}\right\}$.
点评 本题主要考查集合的基本运算,比较基础.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
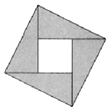 如图,阴影部分是由四个全等的直角三角形组成的图形,在大正方形内随机取一点,这一点落在小正方形内的概率为 $\frac{1}{5}$,若直角三角形的两条直角边的长分别为a,b(a>b),则$\frac{b}{a}$=( )
如图,阴影部分是由四个全等的直角三角形组成的图形,在大正方形内随机取一点,这一点落在小正方形内的概率为 $\frac{1}{5}$,若直角三角形的两条直角边的长分别为a,b(a>b),则$\frac{b}{a}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2-2|x|.
已知函数f(x)=x2-2|x|.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=2AE=2EF=4.
如图,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=2AE=2EF=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com