
Ζ÷Έω ΔΌΘ§”…fΘ®xΘ©=$fΘ®xΘ©=\left\{\begin{array}{l}lnxΘ§xΘΨ0\\ 1Θ§xΓή0\end{array}\right.$÷ΣΘ§xΘΨ0 ±Θ§fΘ®xΘ©=lnxΓ Θ®-ΓόΘ§+ΓόΘ©Θ§≤Μ¬ζΉψfΘ®xΘ©ΓίgΘ®xΘ©=-2Ε‘“Μ«– Β ΐxΕΦ≥…ΝΔΘ§Ω…≈–ΕœΔΌΘΜ
ΔΎΘ§ΝνtΘ®xΘ©=fΘ®xΘ©-gΘ®xΘ©Θ§“Ή÷ΛtΘ®xΘ©=x+sinx-Θ®x-1Θ©=sinx+1Γί0Κψ≥…ΝΔΘ§Ω…≈–ΕœΔΎΘΜ
ΔέΘ§ΝνhΘ®xΘ©=ex-axΘ§Ά®ΙΐΕ‘a=0Θ§aΓΌ0ΒΡΧ÷¬έΘ§άϊ”ΟhΓδΘ®xΘ©=ex-aΘ§“Ή«σx=lna ±Θ§Κ· ΐ»ΓΒΟΉν–Γ÷Βa-alnaΘ§“άΧβ“βΦ¥Ω…«σΒΟaΒΡ»Γ÷ΒΖΕΈßΘ§Ω…≈–ΕœΔέΘΜ
ΔήΘ§ΨΌάΐΥΒΟςΘ§fΘ®xΘ©=2xΘ§gΘ®xΘ©=2x-1Θ§‘ρfΘ®xΘ©-gΘ®xΘ©=1Γί0Κψ≥…ΝΔΘ§Ω…≈–ΕœΔήΘ°
Ϋβ¥π ΫβΘΚΔΌΘ§ΓΏxΘΨ0 ±Θ§fΘ®xΘ©=lnxΓ Θ®-ΓόΘ§+ΓόΘ©Θ§
Γύ≤ΜΡή ΙΒΟfΘ®xΘ©ΓίgΘ®xΘ©=-2Ε‘“Μ«– Β ΐxΕΦ≥…ΝΔΘ§Ι ΔΌ¥μΈσΘΜ
ΔΎΘ§ΝνtΘ®xΘ©=fΘ®xΘ©-gΘ®xΘ©Θ§‘ρtΘ®xΘ©=x+sinx-Θ®x-1Θ©=sinx+1Γί0Κψ≥…ΝΔΘ§Ι Κ· ΐgΘ®xΘ©=x-1 «Κ· ΐfΘ®xΘ©=x+sinxΒΡ“ΜΗω≥–Ά–Κ· ΐΘ§ΔΎ’ΐ»ΖΘΜ
ΔέΘ§ΝνhΘ®xΘ©=ex-axΘ§‘ρhΓδΘ®xΘ©=ex-aΘ§
”…Χβ“βΘ§a=0 ±Θ§Ϋα¬έ≥…ΝΔΘΜ
aΓΌ0 ±Θ§ΝνhΓδΘ®xΘ©=ex-a=0Θ§‘ρx=lnaΘ§
ΓύΚ· ΐhΘ®xΘ©‘ΎΘ®-ΓόΘ§lnaΘ©…œΈΣΦθΚ· ΐΘ§‘ΎΘ®lnaΘ§+ΓόΘ©…œΈΣ‘ωΚ· ΐΘ§
Γύx=lna ±Θ§Κ· ΐ»ΓΒΟΉν–Γ÷Βa-alnaΘΜ
ΓΏgΘ®xΘ©=ax «Κ· ΐfΘ®xΘ©=exΒΡ“ΜΗω≥–Ά–Κ· ΐΘ§
Γύa-alnaΓί0Θ§
ΓύlnaΓή1Θ§
Γύ0ΘΦaΓήeΘ§
Ήέ…œΘ§0ΓήaΓήeΘ§Ι Δέ’ΐ»ΖΘΜ
ΔήΘ§≤ΜΖΝΝνfΘ®xΘ©=2xΘ§gΘ®xΘ©=2x-1Θ§‘ρfΘ®xΘ©-gΘ®xΘ©=1Γί0Κψ≥…ΝΔΘ§Ι gΘ®xΘ©=2x-1 «fΘ®xΘ©=2xΒΡ“ΜΗω≥–Ά–Κ· ΐΘ§Δή¥μΈσΘΜ
Ήέ…œΥυ ωΘ§Υυ”–’ΐ»ΖΟϋΧβΒΡ–ρΚ≈ «ΔΎΔέΙ≤2ΗωΘ°
Ι ¥πΑΗΈΣΘΚ2
ΒψΤά ±ΨΧβΩΦ≤ιΚ· ΐΚψ≥…ΝΔΈ ΧβΘ§άμΫβ–¬Ε®“εΓΑ≥–Ά–Κ· ΐΓ±ΒΡΗ≈Ρν «ΫβΧβΒΡΙΊΦϋΘ§ΩΦ≤ιΒ»ΦέΉΣΜ·ΥΦœκ”κ¬ΏΦ≠ΥΦΈ§ΡήΝΠ”κ‘ΥΥψΡήΝΠΘ§ τ”ΎΡ―ΧβΘ°


 ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | aΘ§bΘ§cΘ§d÷–÷Ν…Ό”–“ΜΗω’ΐ ΐ | BΘ° | aΘ§bΘ§cΘ§d»ΪΈΣ’ΐ ΐ | ||
| CΘ° | aΘ§bΘ§cΘ§d»ΪΕΦ¥σ”ΎΜρΒ»”Ύ0 | DΘ° | aΘ§bΘ§cΘ§d÷–÷ΝΕύ”–“ΜΗωΗΚ ΐ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | ΤφΚ· ΐ | BΘ° | ≈ΦΚ· ΐ | ||
| CΘ° | Φ» «ΤφΚ· ΐ“≤ «≈ΦΚ· ΐ | DΘ° | Φ»≤Μ «ΤφΚ· ΐ“≤≤Μ «≈ΦΚ· ΐ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $-\frac{1}{2}$ | BΘ° | 1 | CΘ° | -2 | DΘ° | $\frac{11}{2}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 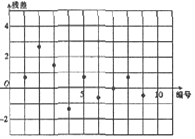 | BΘ° | 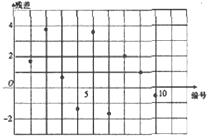 | ||
| CΘ° | 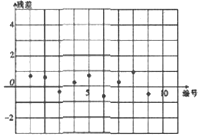 | DΘ° | 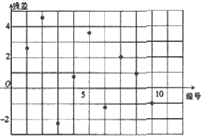 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | Θ®0Θ§4] | BΘ° | Θ®-ΓόΘ§4Θ© | CΘ° | [4Θ§+ΓόΘ© | DΘ° | Θ®4Θ§+ΓόΘ© |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com