
分析 (1)由Sn=2an-3•2n+4(其中n∈N*),n=1时,a1=2a1-6+4,解得a1=2.n≥2时,an=Sn-Sn-1,化为:an-2an-1=3×2n-1,$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{3}{2}$,又bn=$\frac{{a}_{n}}{{2}^{n}}$,可得bn-bn-1=$\frac{3}{2}$.再利用等差数列的定义即可证明.
(2)由(1)可得:an=(3n-1)×2n-1.cn=4n+(-1)n-1λ×2n+1.对任意n∈N*,都有cn+1>cn成立,代入化为:(-1)n-1λ<2n-1,
对n分类讨论即可得出.
(3)dn=$\frac{(3n+5)•{2}^{n-1}}{(3n-1)•{2}^{n-1}•(3n+2)•{2}^{n}}$=$\frac{3n+5}{(3n-1)(3n+2)•{2}^{n}}$=$\frac{1}{(3n-1)•{2}^{n-1}}-\frac{1}{(3n+2)•{2}^{n}}$,利用“裂项求和”方法、数列的单调性即可证明.
解答 (1)证明:∵Sn=2an-3•2n+4(其中n∈N*),∴n=1时,a1=2a1-6+4,解得a1=2.
n≥2时,an=Sn-Sn-1=2an-3•2n+4-$(2{a}_{n-1}-3×{2}^{n-1}+4)$,化为:an-2an-1=3×2n-1,
∴$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{3}{2}$,又bn=$\frac{{a}_{n}}{{2}^{n}}$,可得bn-bn-1=$\frac{3}{2}$.
∴数列{bn}是等差数列,公差为$\frac{3}{2}$,首项为1.
(2)解:由(1)可得:$\frac{{a}_{n}}{{2}^{n}}$=1+$\frac{3}{2}$(n-1),化为:an=(3n-1)×2n-1.
cn=4n+(-1)n-1•λ•$\frac{2{a}_{n+1}}{3n+2}$=4n+(-1)n-1•λ•$\frac{2×(3n+2)×{2}^{n}}{3n+2}$=4n+(-1)n-1λ×2n+1.
对任意n∈N*,都有cn+1>cn成立,∴4n+1+(-1)nλ×2n+2>4n+(-1)n-1λ×2n+1,化为:(-1)n-1λ<2n-1,
n=2k-1(k∈N*)时,化为:λ<22k-2,∴λ<1.
n=2k(k∈N*)时,化为:λ>-22k-1,∴λ>-2.
综上可得:-2<λ<1,又λ为非零整数,∴λ=-1.
∴λ=-1时,使得对任意n∈N*,都有cn+1>cn成立.
(3)证明:dn=$\frac{(3n+5)•{2}^{n-1}}{{a}_{n}•{a}_{n+1}}$=$\frac{(3n+5)•{2}^{n-1}}{(3n-1)•{2}^{n-1}•(3n+2)•{2}^{n}}$=$\frac{3n+5}{(3n-1)(3n+2)•{2}^{n}}$=$\frac{1}{(3n-1)•{2}^{n-1}}-\frac{1}{(3n+2)•{2}^{n}}$,
∴数列{dn}的前n项和为Tn=d1+d2+…+dn=$(\frac{1}{2×1}-\frac{1}{5×2})$+$(\frac{1}{5×2}-\frac{1}{8×{2}^{2}})$+…+($\frac{1}{(3n-1)•{2}^{n-1}}-\frac{1}{(3n+2)•{2}^{n}}$)
=$\frac{1}{2}$$-\frac{1}{(3n+2)•{2}^{n}}$,T1=$\frac{8}{2×5×2}$=$\frac{2}{5}$.
∴$\frac{2}{5}$=${T}_{1}≤{T}_{n}<\frac{1}{2}$.
点评 本题考查了等差数列的通项公式、“裂项求和”方法、递推关系、数列的单调性、不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | “?x≥1,x2<1” | B. | “?x<1,x2≥1” | C. | “?x0<1,x2≥1” | D. | “?x0≥1,x2<1” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
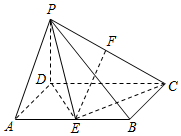 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com