
分析 (1)根据函数的奇偶性设出函数的表达式,根据f(1)=6,f(3)=2,得到关于a,c的方程组,解出即可;
(2)二次函数f(x)是开口朝下,且以y轴为对称轴的抛物线,分类讨论给定区间与对称轴的关系,综合讨论结果,可得答案.
解答 解:(1)∵二次函数f(x)为偶函数,
∴设f(x)=ax2+c,满足f(1)=6,f(3)=2,
∴$\left\{\begin{array}{l}{f(1)=a+c=6}\\{f(3)=9a+c=2}\end{array}\right.$,解得:a=-$\frac{1}{2}$,b=$\frac{13}{2}$,
∴f(x)=-$\frac{1}{2}$x2+$\frac{13}{2}$;
(2)二次函数f(x)=-$\frac{1}{2}$x2+$\frac{13}{2}$是开口朝下,且以y轴为对称轴的抛物线,
当x=0时,函数取最大值$\frac{13}{2}$,
若a<b≤0,则 $\left\{\begin{array}{l}{-{\frac{1}{2}a}^{2}+\frac{13}{2}=2a}\\{-{\frac{1}{2}b}^{2}+\frac{13}{2}=2b}\end{array}\right.$,不存在满足条件的a,b;
若0≤a<b,则 $\left\{\begin{array}{l}{-{\frac{1}{2}a}^{2}+\frac{13}{2}=2b}\\{-{\frac{1}{2}b}^{2}+\frac{13}{2}=2a}\end{array}\right.$不存在满足条件的a,b;
若a<0<b,则2b=$\frac{13}{2}$,解得:b=$\frac{13}{4}$,$\left\{\begin{array}{l}{-{\frac{1}{2}a}^{2}+\frac{13}{2}=2a}\\{a<0}\end{array}\right.$,
解得:a=-2-$\sqrt{17}$,
综上可得:a=-2-$\sqrt{17}$,b=$\frac{13}{4}$.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=cos2x | C. | y=sin3x | D. | $y=tan(2x+\frac{π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
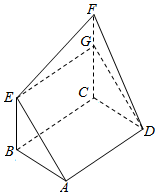 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=$\frac{π}{2}$,AD=$\sqrt{3}$,EF=2.
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF=$\frac{π}{2}$,AD=$\sqrt{3}$,EF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
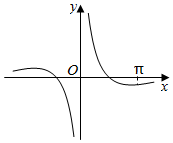
| A. | $f(x)=\frac{{2-{x^2}}}{2x}$ | B. | $f(x)=\frac{sinx}{x^2}$ | C. | $f(x)=-\frac{{{{cos}^2}x}}{x}$ | D. | $f(x)=\frac{cosx}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com