Question

12．一个四棱柱的三视图如图所示，则其表面积为16+8$\sqrt{2}$．

Answer 1

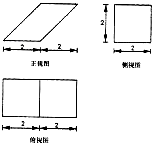
分析 根据几何体的三视图，得出该几何体是底面边长为2的正方形，且上底的一条棱在下底面的射影与下底的一条棱重合，
再根据图中的数据，求出该四棱柱的表面积．

解答 解：根据几何体的三视图，得，
该几何体是如图所示的四棱柱；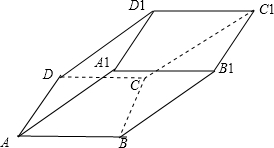
底面ABCD是边长为2的正方形，
且棱A₁D₁在底面ABCD内的射影是BC，
∴该四棱柱的表面积为
2S_{正方形ABCD}+2${S}_{平行四边形A{{BB}_{1}A}_{1}}$+2${S}_{矩形A{{DD}_{1}A}_{1}}$
=2×2²+2×2×2+2×2×$\sqrt{{2}^{2}{+2}^{2}}$
=16+8$\sqrt{2}$．
故答案为：16+8$\sqrt{2}$．

点评 本题以三视图为背景，通过由三视图想象实际几何体及其主要特征，重点考查空间想象能力与推理论证能力．