
分析 本题是一个几何概型,试验的全部结果所构成的区域为{(a,b)|0≤a≤4,0≤b≤3},而构成事件A的区域为{(a,b)|0≤a≤4,0≤b≤3,a≥b},根据几何概型公式得到结果.
解答 解:设事件A为“方程x2+2ax+b2=0有实根”.
则△=4a2-4b2≥0,即a2≥b2.
又∵a≥0,b≥0,
∴a≥b.
试验的全部结果所构成的区域为{(a,b)|0≤a≤4,0≤b≤3},而构成事件A的区域为{(a,b)|0≤a≤4,0≤b≤3,a≥b},即如图所示的阴影部分: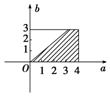
∴P(A)=$\frac{3×4-\frac{1}{2}×{3}^{2}}{4×3}$=$\frac{5}{8}$.
点评 本题给出含有字母参数的一元二次方程,求方程有实数根的概率.着重考查了一元二次方程根的判别式、不等式表示的平面区域、面积公式和几何概型计算公式等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
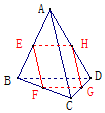 已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,
已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
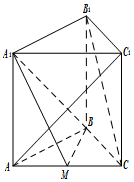 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=N*,B=N*,f:x→|x-3| | |
| B. | A={平面内的圆},B={平面内的三角形},f:作圆的内接三角形 | |
| C. | A={x|0≤x≤2},B={y|0≤y≤6},f:x→y=$\frac{1}{2}x$ | |
| D. | A={0,1},B={-1,0,1},f:A中的数开平方根 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1008 | C. | 1009.5 | D. | 1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,4) | C. | (1,2) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com